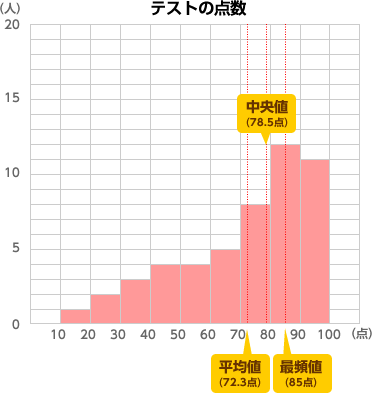
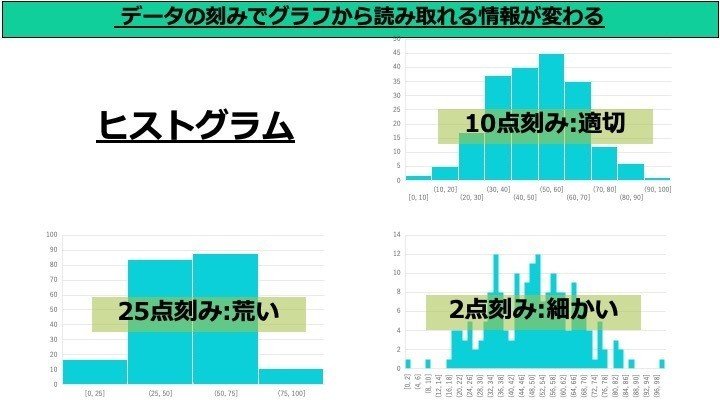
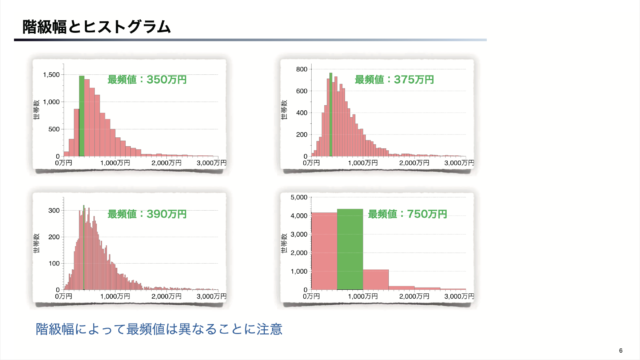
最頻値: 度数のもっとも多い階級の真ん中の値 中央値: 大きさの順に並べたときの中央の値(資料の総数が奇数の場合は、大きさの順に並べたときの中央の値、資料の総数が偶数の場合は、中央にある2つの値の平均値を中央値とする)ヒストグラム を解釈するに ピークは最も一般的な値を示しています。 ヒストグラムの中央はほぼ同じですが、いくつかのヒストグラムはより大きく、広がりもあります。大きな広がりは、これらの機械の瓶詰めがあまり一定していないことを示します。ヒストグラムで与えられたデータのみから平均値を計算するには,各階級に対応する代表値と度数 を用いて計算する.各階級に対応する代表値が(m1,m2,··,mn) で与えられたとすると,以下の式 により
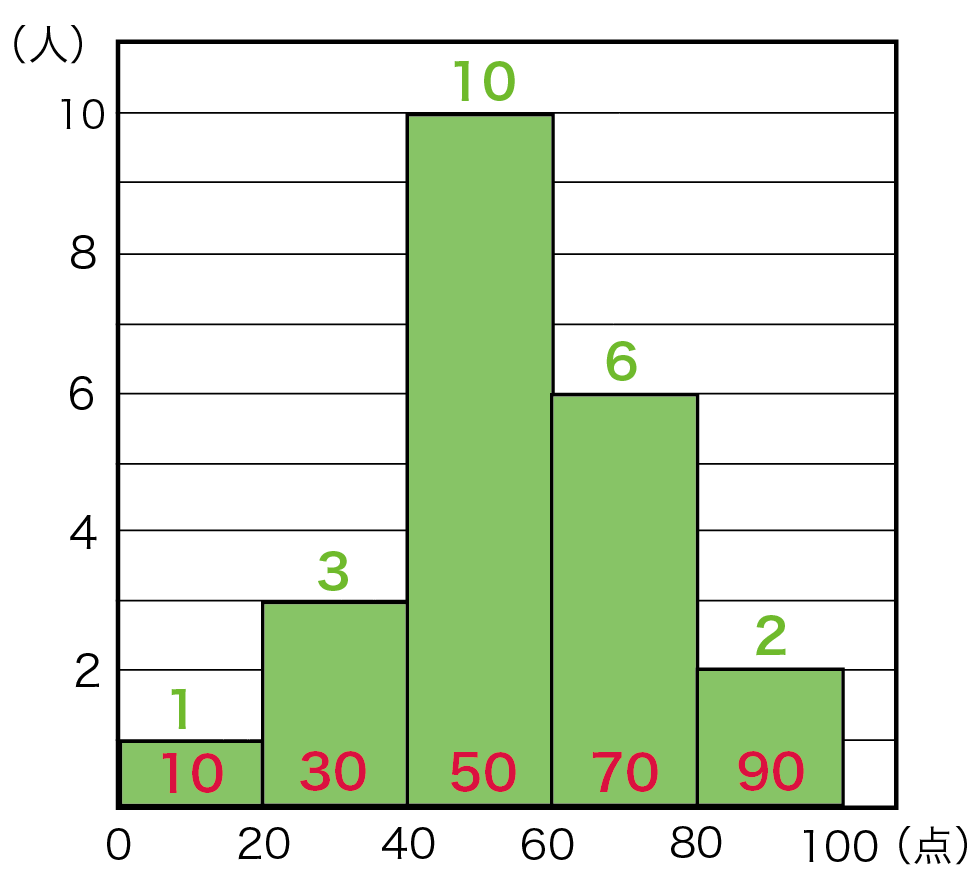
ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
ヒストグラム 階級 中央値
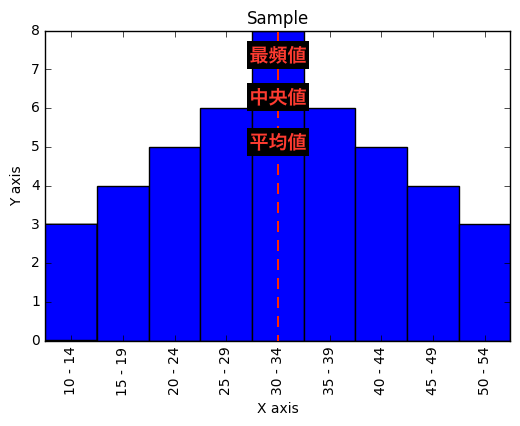
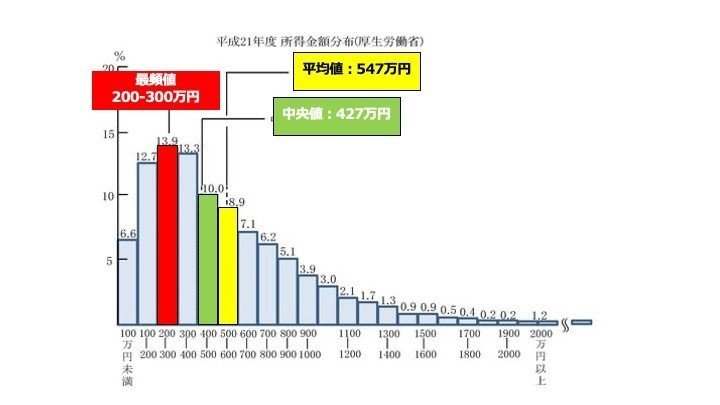
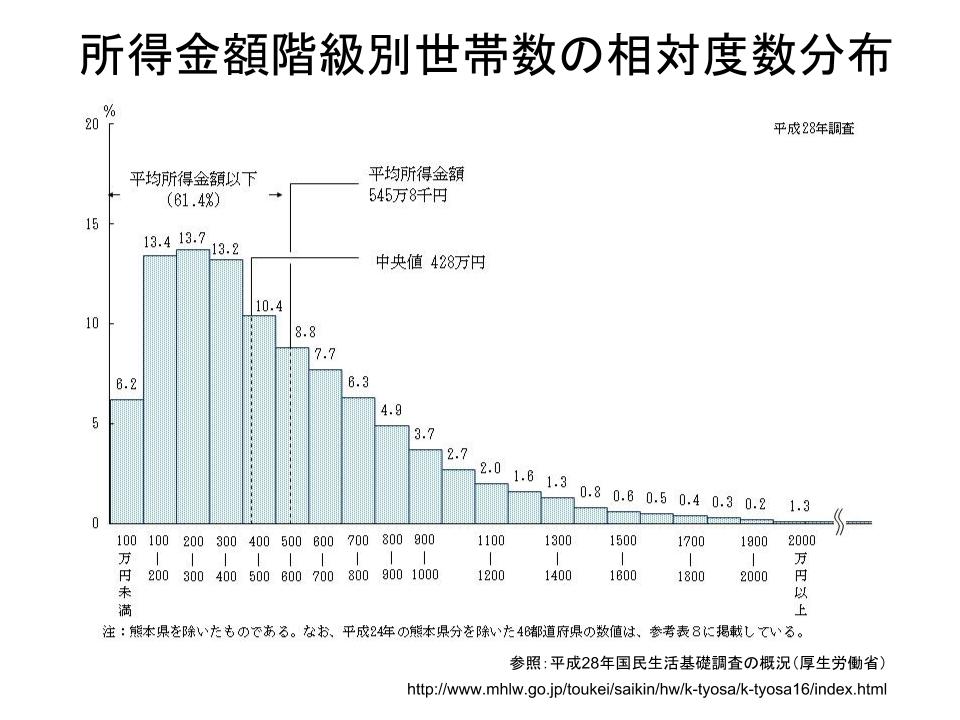
ヒストグラム 階級 中央値-1組のヒストグラムのように山が一つで左右対称の分布の場合、「平均」「 中央値 」「 モード 」はすべて同じ値になります。 一方、2組のヒストグラムのように山が一つでも、分布が左右対称ではなく左に偏っている(=右に裾を引いている)場合、「平均」「中央値」「モード」は一致せず、右から順番で並ぶことが多くなります。 このデータの場合、「平均:157 そこで、今回は 度数分布表(ヒストグラム)だけでも入手できた時 に、そこから3つの値を推定するPythonプログラムを紹介します。 例えば、以下の給与統計では「平均値」は分かりますが、「中央値」「標準偏差」が不明です。



ヒストグラムとは 作り方 書き方 や階級 データ区間の決め方 受験辞典
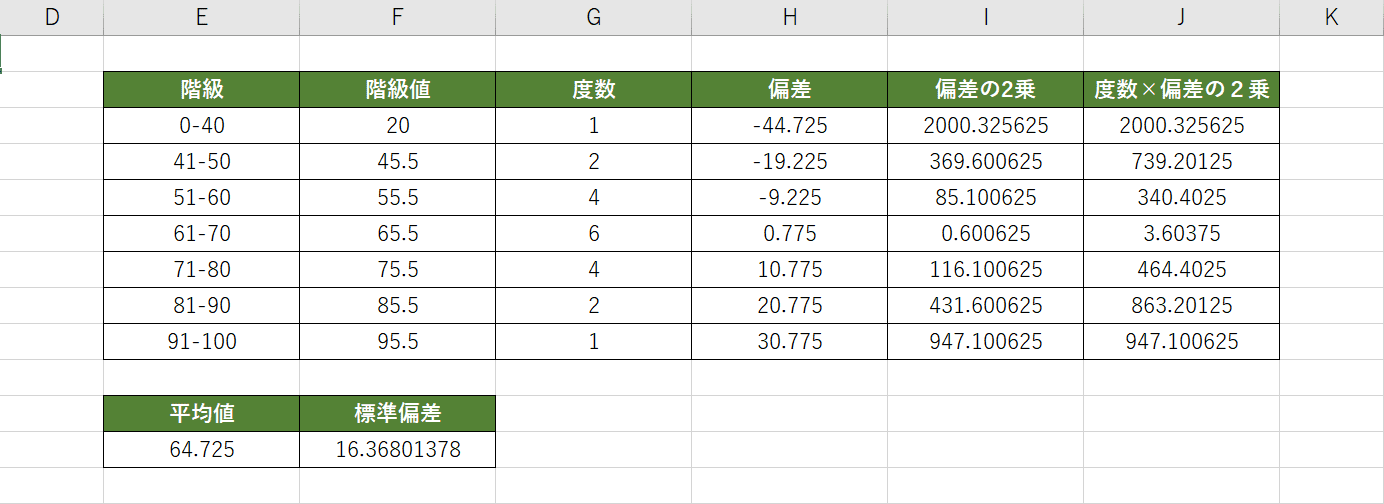
2 階級幅はまず00とし、その後1000に変更します。 3 ヒストグラムと同時に、平均値、中央値、及びデータの個数を表示します。 エクセルによるヒストグラムの作成 お題に沿ったヒストグラムの作成をエクセルで行いました。 ヒストグラムから階級値を使って平均値と標準偏差を求めよう そのデータがどのような分布をしているのかを知るためには、 ヒストグラム を作るのが一番です。 ヒストグラムを正しく作る簡単な方法 という事で、私なんかはよく材料メーカーから度数データを値の大きさの順に並べたとき,中央の位置にくる値を中央値という。 この問題では,ファミリーレストランを利用した25組のデータについて考えます。 25組は奇数個なので,真ん中は13番目の組になります。 そこで,人数の少ない方から並べたときの13番目の組の人数が中央値です。 ヒストグラムより人数の少ない順に並べると,下のようになります。 13
階級 値 世 帯 数 階級幅 ~0 157 239 0~250 225 368 18 139 239 86 50 y u 最低収入が不明 157 2 0 x 0 114 86 x 114 x これをヒストグラムの棒の高さとする:級 幅の違いを考慮に入れてやる。階級幅が 広いほど,棒は低くなる。 250 0 50 368 y u u50 階級幅 度数 中央値とは、要は真ん中の値です。 ヒストグラムに書き込んである数字は各階級の「度数」でしょう。 合計は、8 6 5 4 4 19 8 1 = 55、よって28番目がちょうど真ん中になります。28番目のデータは250~300の階級のところにあります。よって、この階級の階級値が中央値数学17章データの分布「ヒストグラムや代表値の意味」<基本問題①> (令和3年度以降は小学校6年の内容の復習として活用ください。 組 番 名前 1次の2つの表は,ある中学校1年生人のテスト前日の家庭学習時間を,グループAと
① 中央値は軽いほうから8 番目の生徒の体重だから46kg です。 答え 46kg ② 最頻値は,47kg 以上51kg 未満の階級の階級値(真ん中の値)だから 49kg となります。 答え 49kg ③ ①より15人の体重の中央値は46kg で,この中央値と比較して考えます。44kg は 階級値とは、階級を代表する値のことで、階級の中央の値を取ります。 例えば、階級「 ≦ x < 30」の階級値は 25、階級「30 ≦ x < 40」の階級値は 35 となります。• 中央値は50%点,第1四分位点は25%点 m番目の階級の階級値 番目の階級の度数 階級幅 番目の階級の累積度数 標本数 番目の階級の下限値 m m p m × ⎭ ⎬ ⎫ ⎩ ⎨ ⎧ − − × 1 100 3.3.2本当の式の説明 • ある階級に属すデータが階級内に均等分布



経営を学ぶ 経営学 Mba 起業
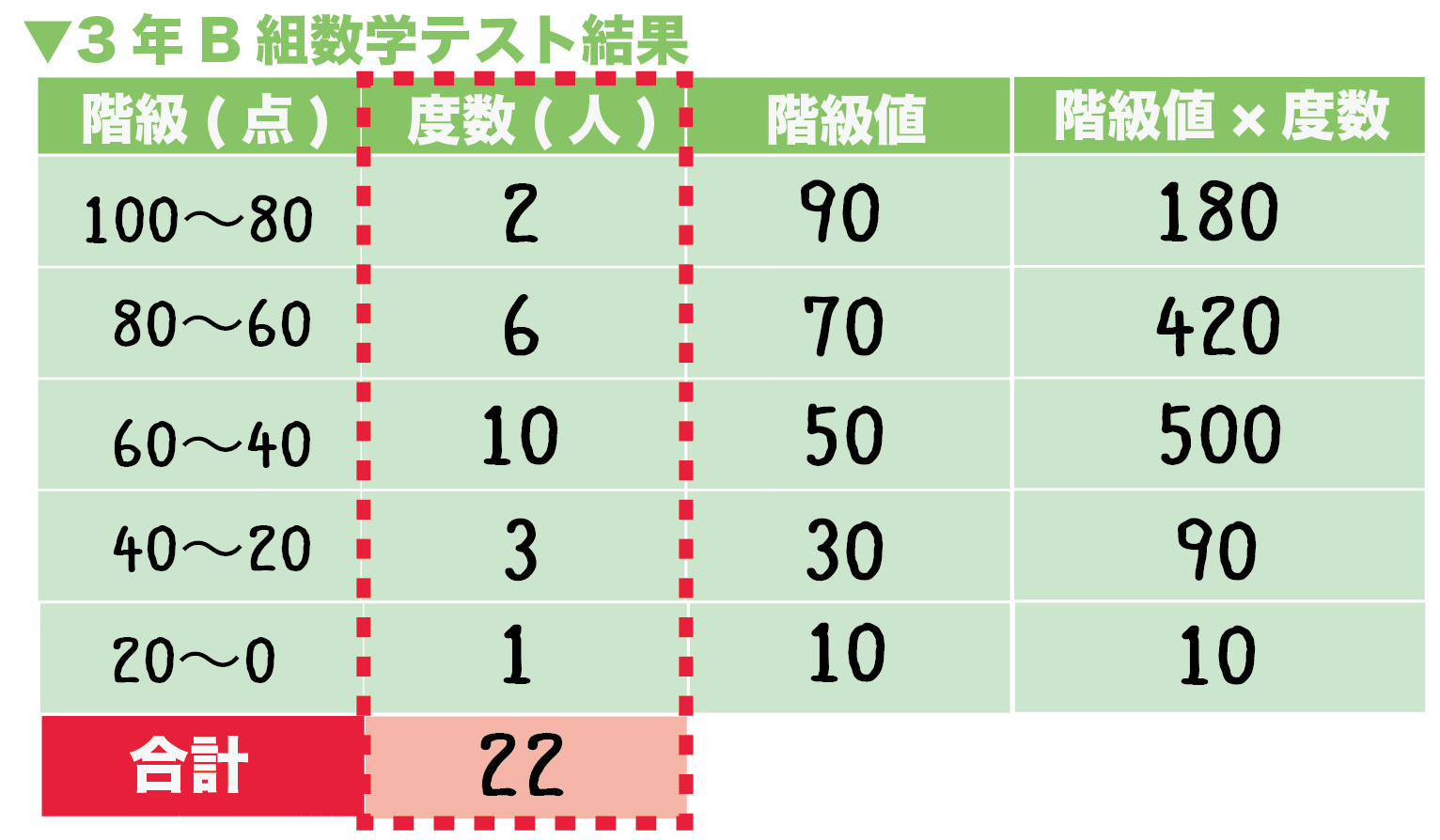



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
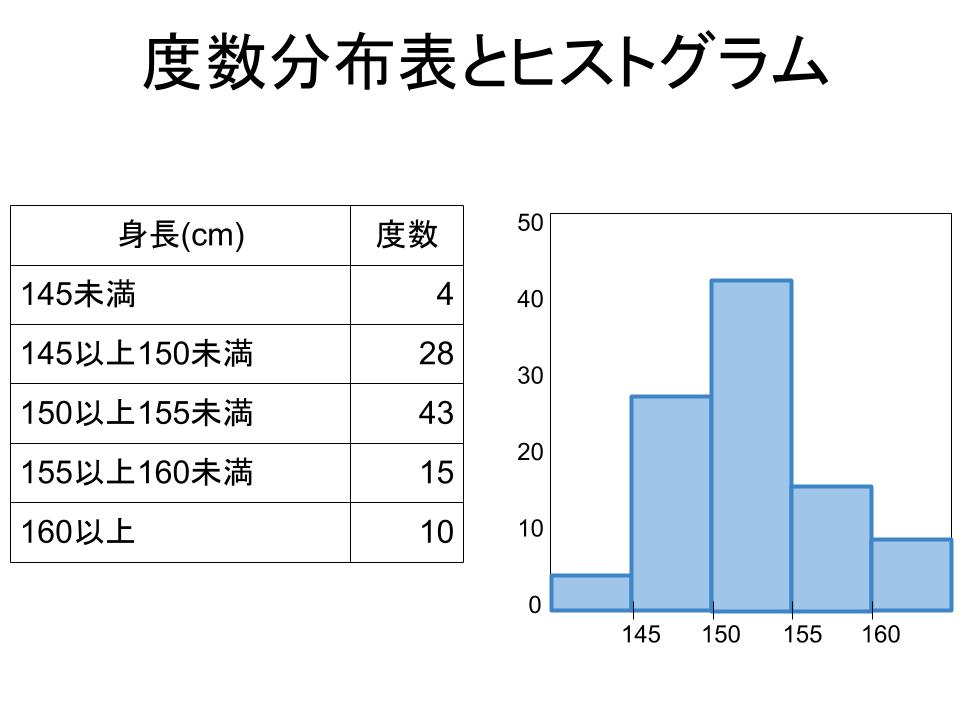
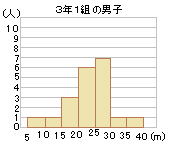
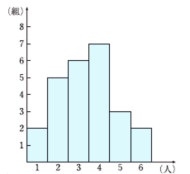
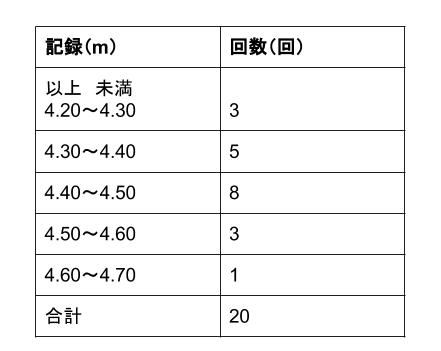
中央値資料の値を大きい順に並べたとき、中央の値を中央値(メジアン)といいます。奇数個の中央値例\(9\) 人の生徒の通学時間(分)\(6, 13 , 15 , 10 , 12 , 24 , 15 , 8 , 18 \)この \(9\) 人の通学時間の中央値を求めてみましょう。\(9\) 個の考え方 階級値は,階級の中央の値。階級の幅は,区間の幅。 解き方 ⑴ 145-140=5,150-145=5,と 5 cm ごとに区切られ ている。 答 5 cm ⑵ クラスの合計人数は, 4+7+11+9+6+3=40 (人) 答 40人ヒストグラムでは 、横の軸 (x軸)に記載する数値を「階級」と呼び、データを区切った区間を記入 します。



分布 平均 分散 しまね統計情報データベース
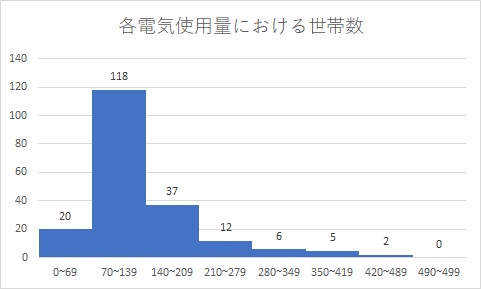



ヒストグラムから階級値を使って平均値と標準偏差を求めよう シグマアイ 仕事で使える統計を
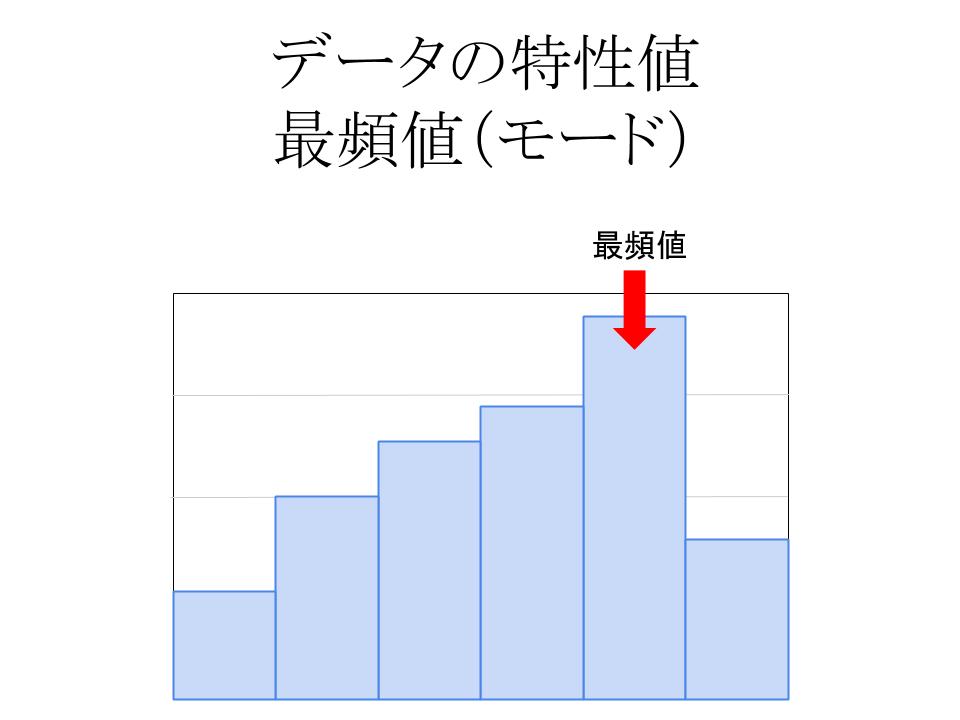
データの代表値 中央値と四分位数 今日やる様々な表現方法 分 位 数 タ イ プ岩薩林確率・統計(少) 平 均 タ イ プ岩薩林確率・統計§12 岩薩林確率・統計(少) 代表値 中央値,四分位数 平均値 最頻値(離散デー タの, ヒストグラ ムの) 散布度 範囲=レンジ, 四データの代表値 ~中央値~ 中央値は、データ全体を順番に並べたときの真ん中の 値です。平均値に比べて、外れ値(他の値から大きくは ずれたもの)の影響を受けにくいのが特徴です。 データの代表値 ~最頻値~ 最頻値とは、最も度数が多い階級の値をいいます。「い19Excel#10 ヒストグラムと中央値 株価データの終値について、「 ヒストグラム ( histogram;度数分布) 」 を作成します。 縦軸に度数、横軸に階級(ビン:bin)をとった棒グラフで表した統計 グラフ の一種で、データの分布状況を視覚的に認識するために




ヒストグラムの意味と書き方 平均値 中央値の求め方を解説




ヒストグラム Histogram A T
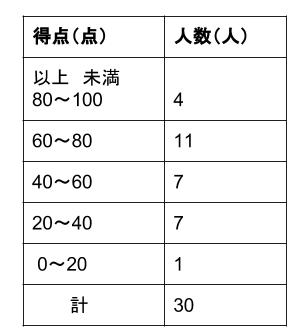
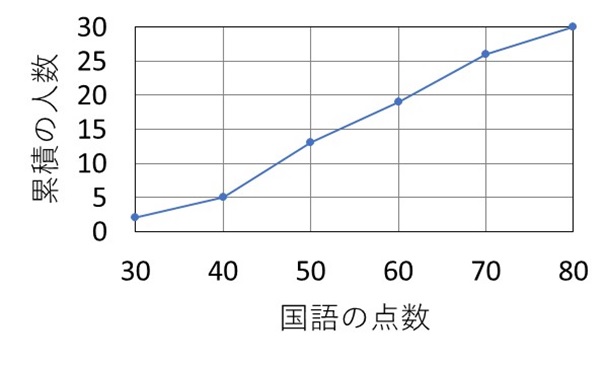
5 ヒストグラムの作成(1) 度数分布表からのヒストグラムの作成 注意点 異なる階級幅が混在している。 原則:柱の面積が度数に比例するように描く。 ヒストグラムの縦軸を密度にすると安全である。 密度=相対度数÷階級幅 開放間隔の階級の存在 開放間隔:下限または上限が明示されていない復習データの分布 ヒストグラムと箱ひげ図の対応 L01Q5 Quiz解答ヒストグラムと箱ひげ図 1Q2= (6070)=2 = 65 Q1は30 50 55 55 60 の中央値なので55 Q3は70 70 70 75 100の中央値なので70 Q3 Q1 = 15 15 15 = 225 (これは描かない) 55 225 以下や, 以上の値は外れ値 生徒の数は全員で 30 人ですので、中央の値である 15 番目の点数を読み取ります。 上図のように累積度数が 15 の値を読み取ると、53 点ということが分かります。 よって、国語の点数の中央値は 53 点です。




19 Excel 10 ヒストグラムと中央値 Johousyori2



まなぼう統計 統計を知ろう 学ぼう データの特徴 変化をとらえよう 資料のちらばりを表す 代表値
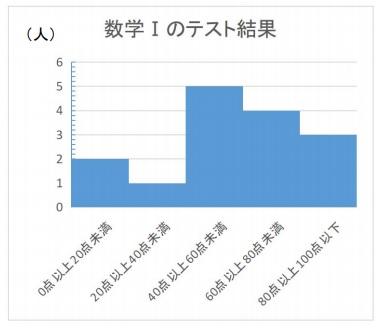
中央値 中央値とは、順番にデータを並べた際に中央にある値のことです。たとえばデータが100ある場合は、その50番目と51番目の階級値を求めます。それぞれを合計し、2で割ることで中央値が算出されます。 (中央の値1つ目+中央の値2つ目)÷2 最頻値ヒストグラムの中央値は「中央のデータが属する階級の階級値」 したがって、中央値は50点となります。 データの中央値とヒストグラムの中央値は求め方が少し異なります。 データの中央値について詳しく知りたい方は「中央値の求め方とメリット」を参考にしてください。 ヒストグラム<練習問題> 手順1:データを昇順に並べ変えをし、最大値と最小値をみつけます。 手順2:この最大値と最小値の間を一定値で区切ります。 この区切りを「 階級 」と呼び、階級を代表する値として一般的には中央値が選ばれ「 階級値 」と呼びます。



プログラマーのための統計学 平均値 中央値 最頻値 Qiita




ヒストグラムの意味と書き方 平均値 中央値の求め方を解説
中央値の求め方(奇数) データの数が奇数個の場合には、ちょうど真ん中に位置する値を見つけることができます。 そのため、真ん中に位置する値が何番目になっているのかを求めることができれば、すぐに中央値が分かりますね! 中央値は何番目 中央値とは、データを大きさ順に並べたとき、ちょうど真ん中にくる値のことでした。 ヒストグラムから求める場合は、 データの個数のちょうど真ん中の値が属する階級の階級値 を中央19Excel#10 ヒストグラムと中央値 注意 ヒストグラム ( histogram )とは、 度数分布 ともいい、 縦軸に度数、横軸に階級(ビン:bin 最後に、出来上がった複合グラフに、中央値



Q Tbn And9gct9g81v6fbuxe2zy40zobgjz7pv4jyf9dpik7xrlwfhfckmjg0k Usqp Cau



資料の整理
〇一般に,資料の個数が奇数個の場合は,大きい方から数えても小さい方から数えても中央に来る値が1つに決まり,その値が中央値です. 例5人の体重 (kg) 453, 471, 514, 537, 576 この例では,中央値は 514 です.




機械学習の統計学 度数分布表 ヒストグラムと平均値 中央値 最頻値について ししまる みらいのクルマをつくる人 Note



ヒストグラムの意味と書き方 平均値 中央値の求め方を解説



機械学習の統計学 度数分布表 ヒストグラムと平均値 中央値 最頻値について ししまる みらいのクルマをつくる人 Note



Www Stat Go Jp Dss Getting Pdf Index Pdf
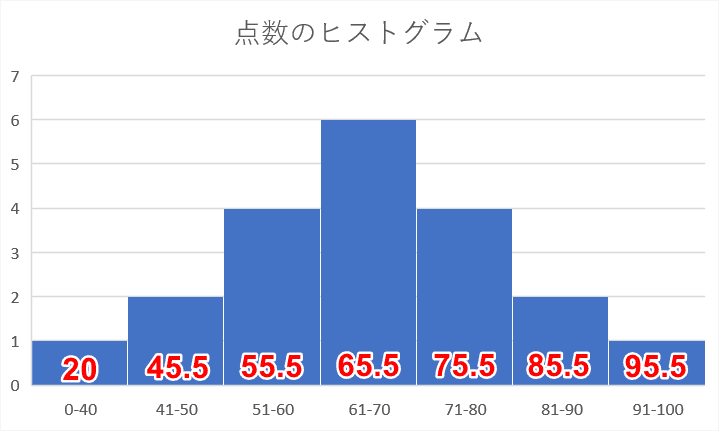



ヒストグラムとは エクセルによるヒストグラムの作り方 書き方 Office Hack



3 2 平均 中央値 モードの関係 統計学の時間 統計web




数学における度数分布表とヒストグラムとは 中央値 最頻値も 高校生向け受験応援メディア 受験のミカタ




中学数学 3分でわかる 階級値 ってなに Qikeru 学びを楽しくわかりやすく



中心的な傾向を捉える



Q Tbn And9gcrucc9oonrnsr8xt7hwgg24wwhri7 M4v0tilyyttjwqnmgepnl Usqp Cau



資料整理の用語 中学から数学だいすき
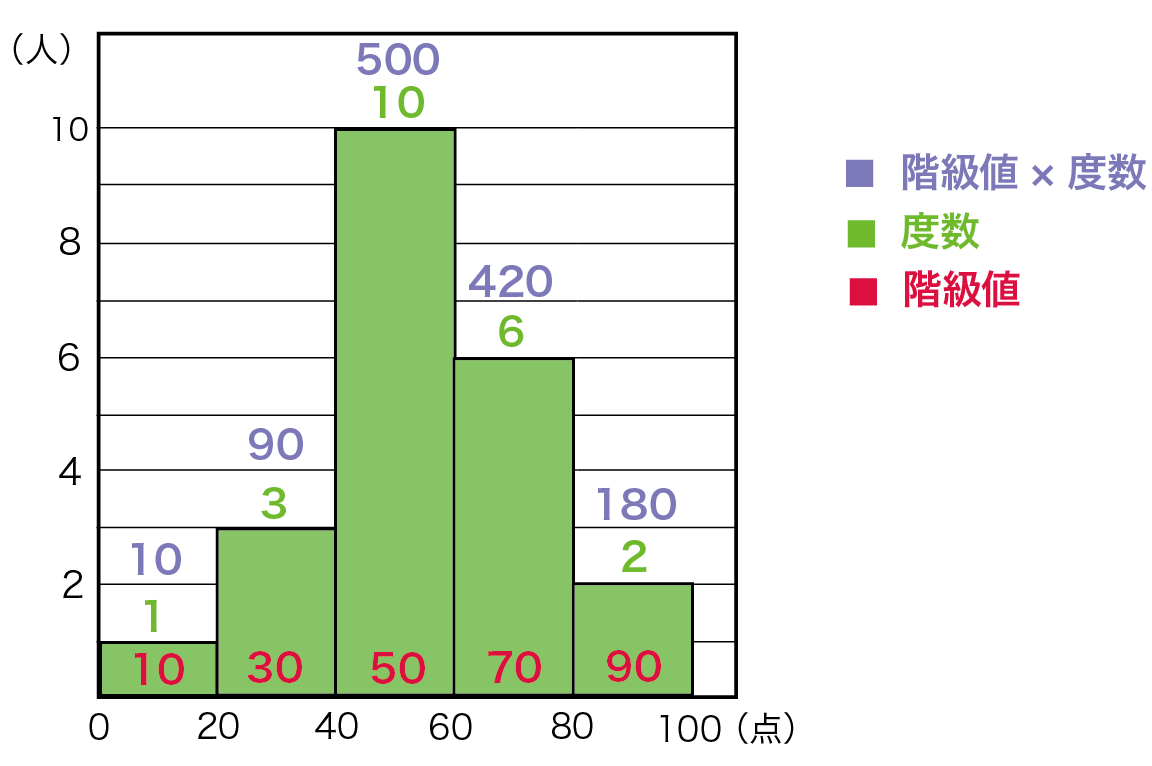



ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



ヒストグラムとは 作り方 書き方 や階級 データ区間の決め方 受験辞典
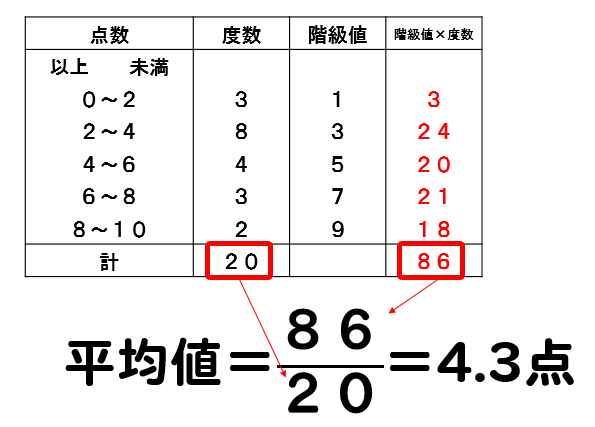



中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ



3 3 平均 中央値 モードの使い方 統計学の時間 統計web



機械学習の統計学 度数分布表 ヒストグラムと平均値 中央値 最頻値について ししまる みらいのクルマをつくる人 Note



経営を学ぶ 経営学 Mba 起業



ヒストグラムとは 作り方 書き方 や階級 データ区間の決め方 受験辞典




中学数学 最頻値 モード の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座



中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su



平均値 中央値 最頻値の違い 求め方 使い分け 計算問題 受験辞典



分布 平均 分散 しまね統計情報データベース



ヒストグラムとは エクセルによるヒストグラムの作り方 書き方 Office Hack



センター数学iib 統計資料の整理 08追試験 09本試験 問題と解説



3 2 平均 中央値 モードの関係 統計学の時間 統計web



ヒストグラムとは 作り方 書き方 や階級 データ区間の決め方 受験辞典




ヒストグラムの意味と書き方 平均値 中央値の求め方を解説




ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



ヒストグラムとは エクセルによるヒストグラムの作り方 書き方 Office Hack




ヒストグラム Wikipedia



1



最頻値を求める 中学から数学だいすき



ヒストグラムから求める 平均値 中央値 最頻値 苦手な数学を簡単に



2 3 階級幅の決め方 統計学の時間 統計web



Excel エクセル でのヒストグラム 度数分布図 の作り方 Prau プラウ Office学習所



経営を学ぶ 経営学 Mba 起業



ヒストグラム
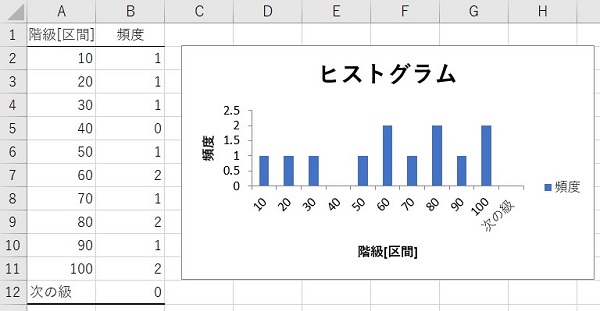



画像付き エクセルでヒストグラム作る方法 Frequency関数で作った表から作る方法も ワカルニ




1 35 Descubre Como Resolverlo En Qanda




中央値 Wikipedia
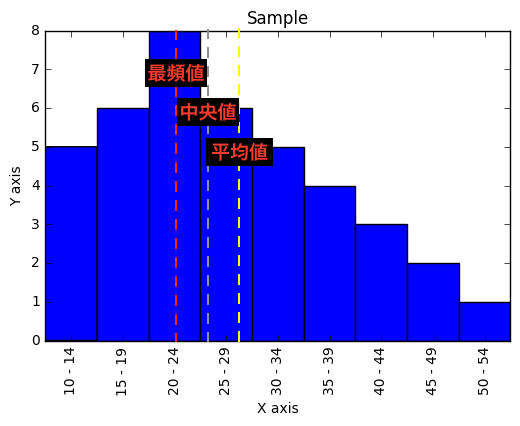



プログラマーのための統計学 平均値 中央値 最頻値 Qiita
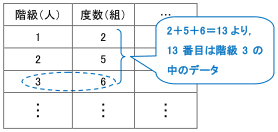



ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座
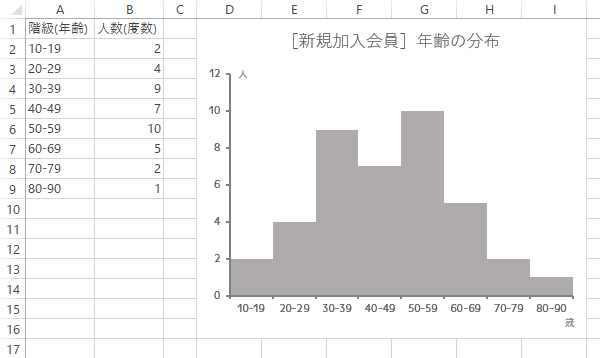



Excelによるヒストグラム 作図のためのtips 数値ラベルを階級の境界に表示する



中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su



中学 相対度数の計算方法と問題はこれでバッチリ 数スタ




中学数学 資料の散らばりと代表値
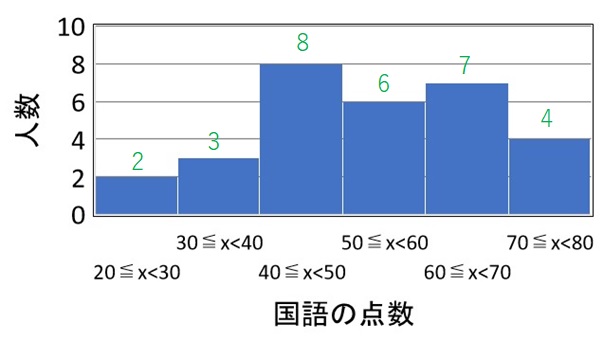



ヒストグラムの中央値の求め方 科学センスを目指して



レポート 社会人のためのデータサイエンス入門 Week2 統計学の基礎 Developersio



3 2 平均 中央値 モードの関係 統計学の時間 統計web



ヒストグラムの中央値の求め方 科学センスを目指して




代表値 平均値 中央値 最頻値 の意味と違い 数学fun
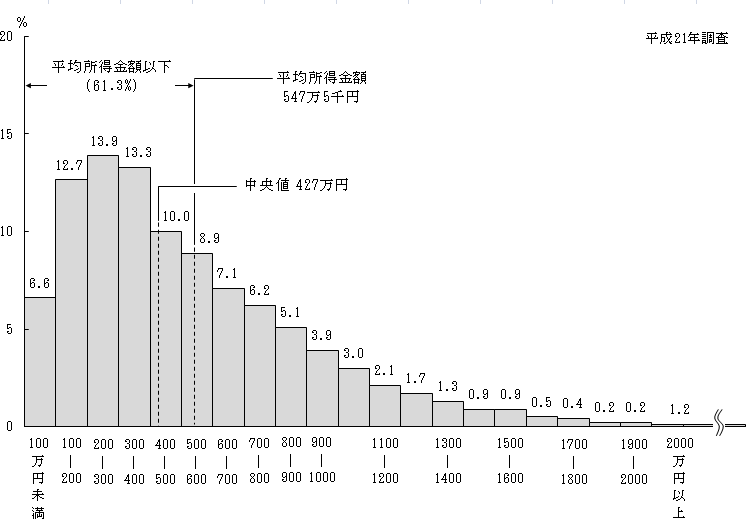



2 所得の分布状況 厚生労働省
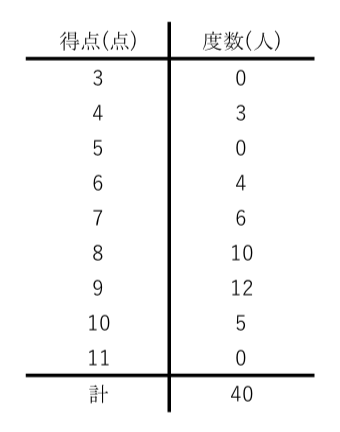



ヒストグラムから求める 平均値 中央値 最頻値 苦手な数学を簡単に
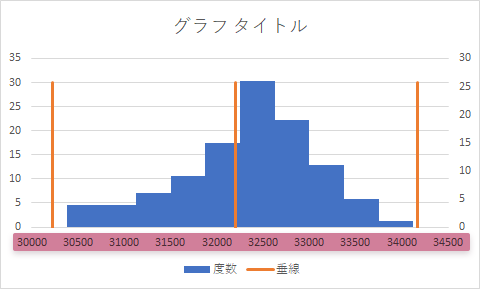



Excelによるヒストグラム 作図のためのtips 平均 規格値などの垂線を重ねる
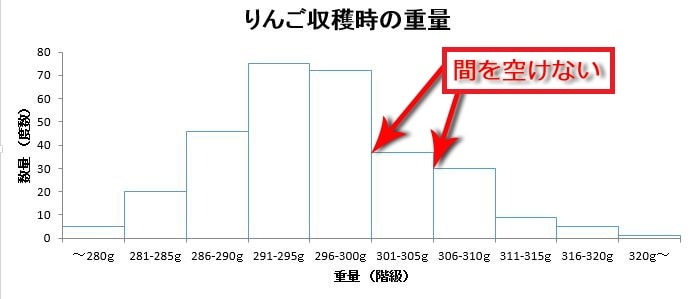



ヒストグラムとは ヒストグラムの書き方 作り方 や分布図の見方を徹底解説 Backlogブログ
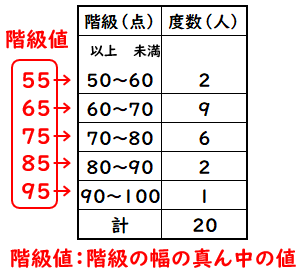



代表値 平均値 中央値 最頻値 の意味と違い 数学fun




基礎統計学の勘どころ 1 度数分布表とヒストグラム 箱ひげ図 十の並列した脳
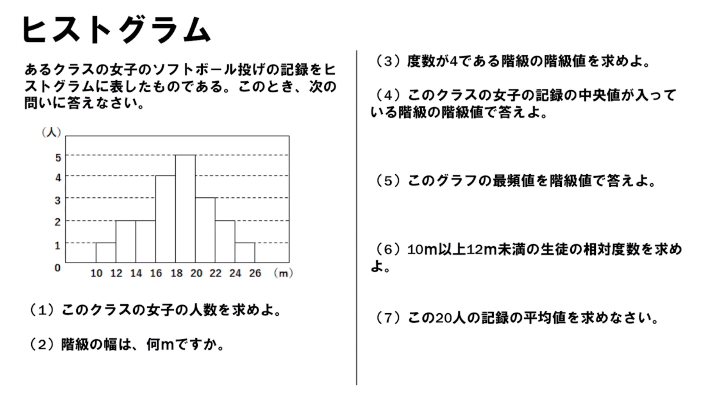



中1数学 資料の整理のポイントと定期テスト予想問題 Pikuu
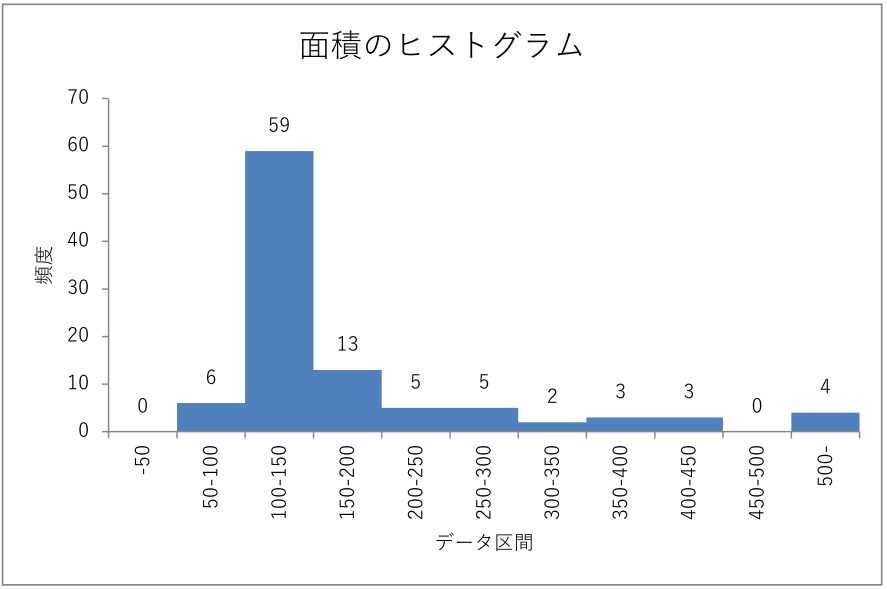



ヒストグラム 度数分布図 の階級の幅 データ区間の決め方 不動産実務tips



中心的な傾向を捉える




ヒストグラムの型と事象 2



経営を学ぶ 経営学 Mba 起業




度数分布とヒストグラム Jsciencer
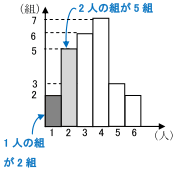



ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座




ヒストグラムの意味と書き方 平均値 中央値の求め方を解説




高校数学 ヒストグラム とは 例題編 映像授業のtry It トライイット
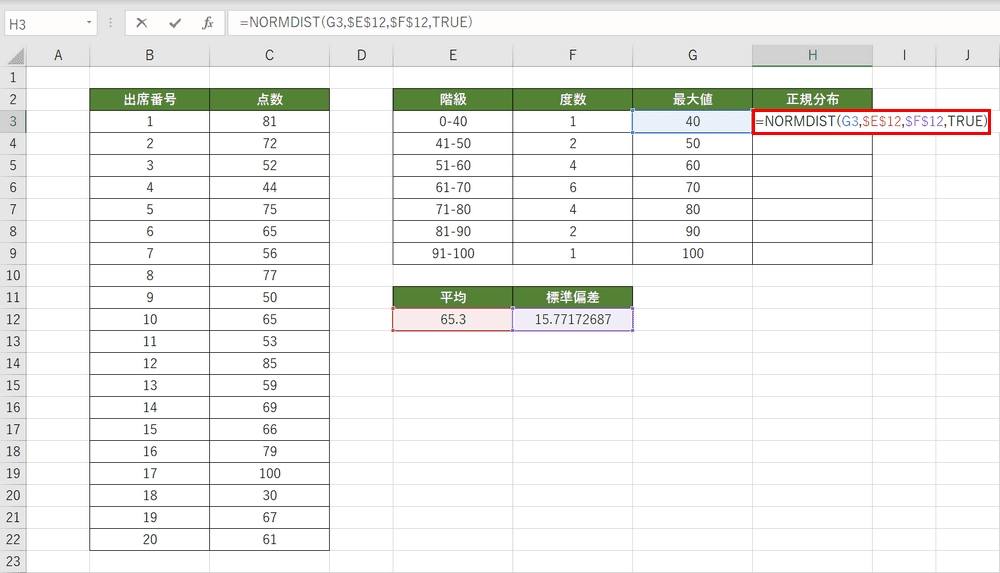



ヒストグラムとは エクセルによるヒストグラムの作り方 書き方 Office Hack
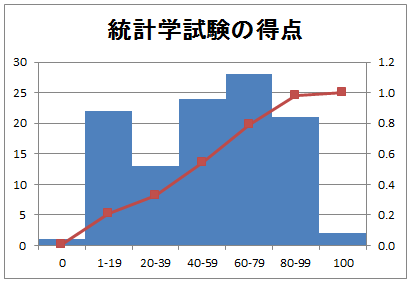



Excelによるヒストグラムの作り方 ブログ 統計web



3 2 平均 中央値 モードの関係 統計学の時間 統計web
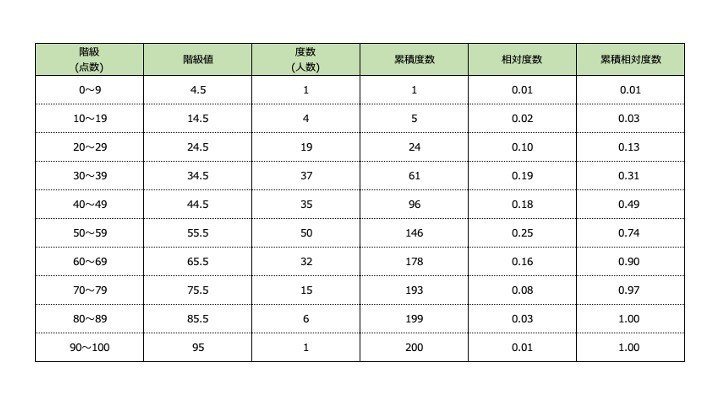



機械学習の統計学 度数分布表 ヒストグラムと平均値 中央値 最頻値について ししまる みらいのクルマをつくる人 Note




数学における度数分布表とヒストグラムとは 中央値 最頻値も 高校生向け受験応援メディア 受験のミカタ
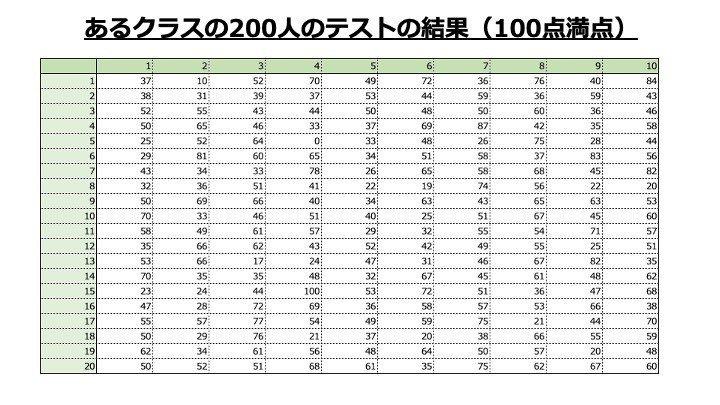



機械学習の統計学 度数分布表 ヒストグラムと平均値 中央値 最頻値について ししまる みらいのクルマをつくる人 Note
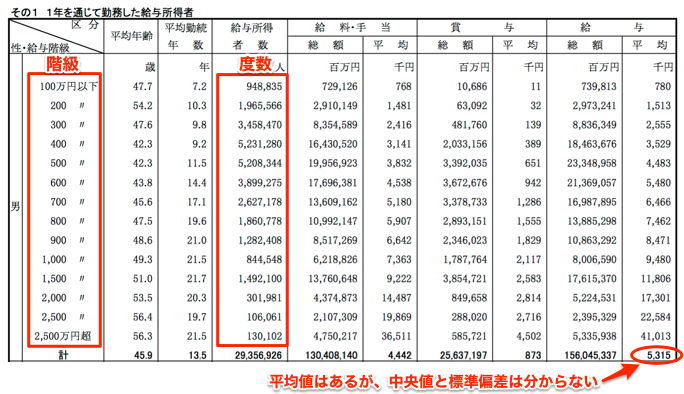



度数分布表からpythonで平均値 中央値 標準偏差を推定する方法 ガンマソフト株式会社




Excelによるヒストグラム 作図のためのtips 正規分布曲線を重ねる




ヒストグラムの意味と書き方 平均値 中央値の求め方を解説




ヒストグラムの意味と書き方 平均値 中央値の求め方を解説



1



Www Pref Kanagawa Jp Documents K4 B Pdf




中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




度数分布とヒストグラム 高校物理の備忘録



下の写真のヒストグラムの 平均値 最頻値 10分以上分未満の相対度 Yahoo 知恵袋



1 4 Ad Descubre Como Resolverlo En Qanda



ヒストグラムから中央値を求める方法が 分かりません また その値の階級は Yahoo 知恵袋




ウーバーイーツ 距離料金の平均 中央値 モードの関係をみる 統計学習ログ 技術学習ジャンキー



ヒストグラムとは ヒストグラムの書き方 作り方 や分布図の見方を徹底解説 Backlogブログ



中学1年数学練習問題 代表値 平均値 階級値 中央値 最頻値の問題



このヒストグラムから中央値を求めるときの過程を教えてほしいです Yahoo 知恵袋




Pythonでヒストグラムの中央値を求める方法を現役エンジニアが解説 初心者向け Techacademyマガジン




ヒストグラムと平均線 Tableau の場合 データ可視化のアイデア帳



度数分布とは 表や多角形の作り方 平均値 中央値 最頻値の問題 受験辞典
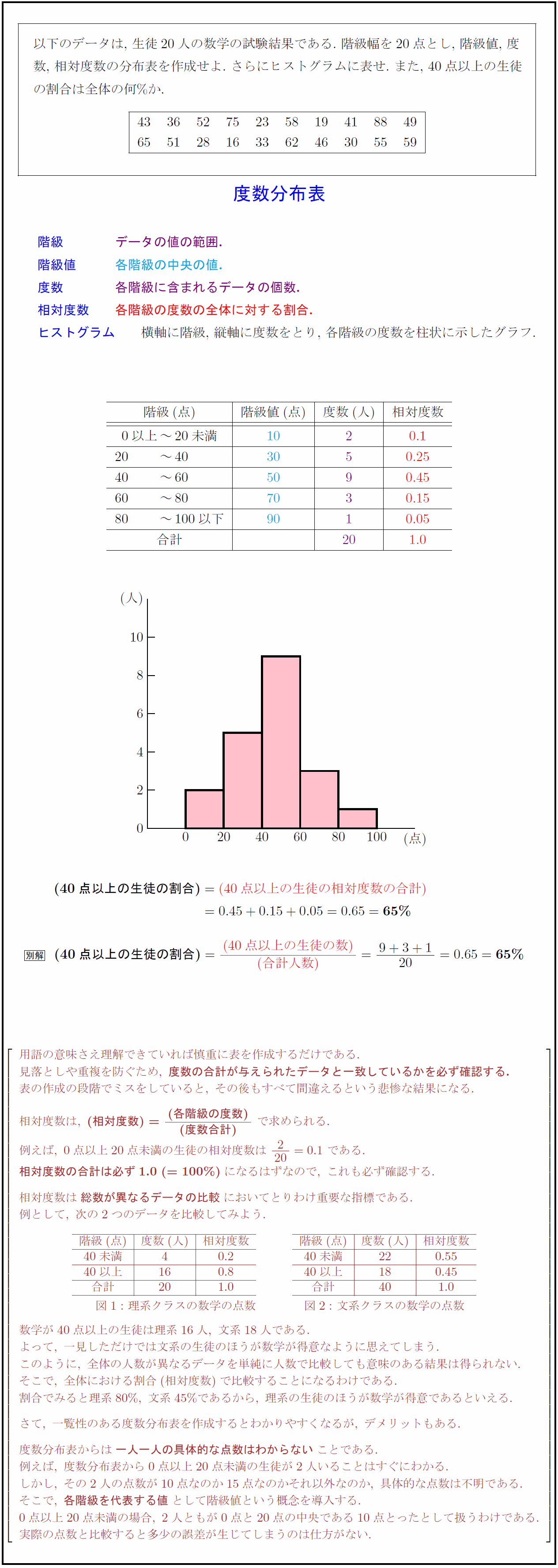



高校数学 度数分布表 階級値 相対度数 ヒストグラム 受験の月



0 件のコメント:
コメントを投稿