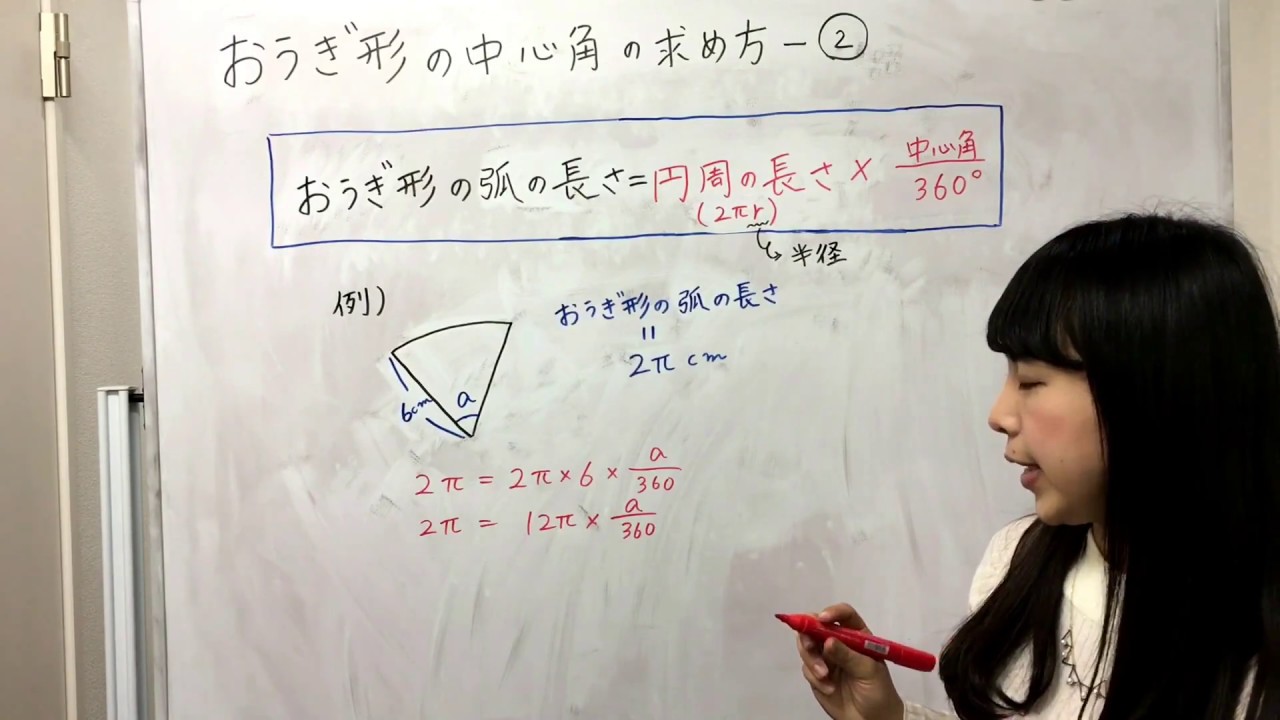
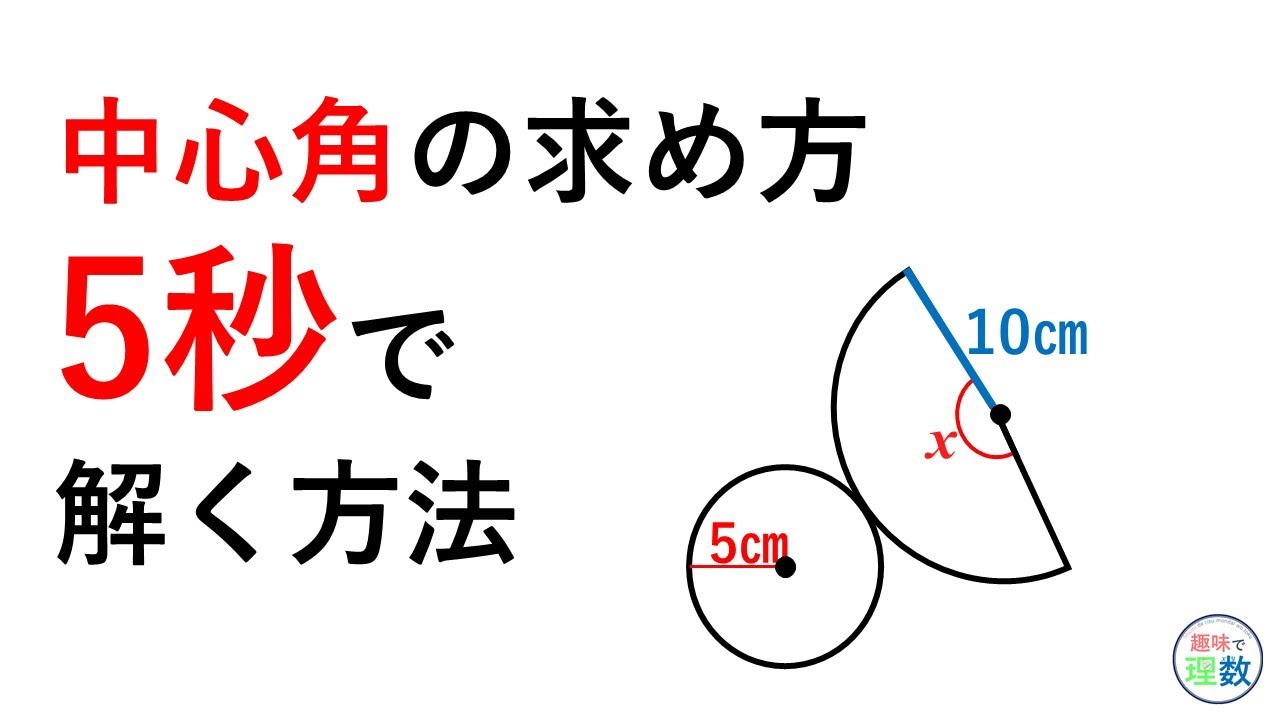
半径16cmで中心角315°のおうぎ形の弧の長さを求めよ。 半径12cmで中心角80°のおうぎ形の面積を求めよ。 半径10cmで中心角°のおうぎ形の面積を求めよ。 半径 9 2 cmで中心角160°のおうぎ形の面積を求めよ。 半径3㎝、中心角1°のおうぎ形がある。 弧の長さを · 扇形の中心角の求め方なのですが、下の式を解くとなんでπが消えるのですか。移項はしないのですか。バカ ベストアンサー:8π=2π×6×x/360 8π=12πx/360 両辺に360をかける 12πx=π 両辺を12πで割る x=240 6 3/28 1040 匿名投稿 数学 半径4cm 面積6πcm²の扇形の中心角の求め方を教えてください問題側面のおうぎ形の中心角の大きさを求めなさい。 側面のおうぎ形は半径 $5 \rm cm$ の 円の一部 といえます。よって、 円周と弧の長さの比率 から、おうぎ形の中心角を求めることができます。 半径 $5 \rm cm$ の円周なので、$2×5×π=\textcolor{blue}{10π}$
Http S Ir Sap Hokkyodai Ac Jp Dspace Bitstream 1 69 2 Kyoiku 14 Pdf
扇形の中心角求め方
扇形の中心角求め方- · 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ 扇形 中心角 求め方 母線 扇形 中心角 求め方 母線扇形の半径の求め方教えてください! なんか、公式みたいなやつ 円とおうぎ形 0 回答 名無し 2年弱前 (弧の長さ)=(半径)×(円周率)×(中心角)÷180 なの · 数学 扇形の中心角と円弧の求め方を教えて下さい(~_~;) 双方わからない状態です。(半径はわかります) みんなのq&a 3,100万人が利用!最大級のq&aコミュニティ 専門家のq&a みんなの悩みに専門家が回答します 著名人のq&a 話題の著名人が教えてくれる自分磨きのq&a why okwave q&aをとおして




円すいの側面積と展開図の中心角 たぬぬ塾 中学校の先生たち
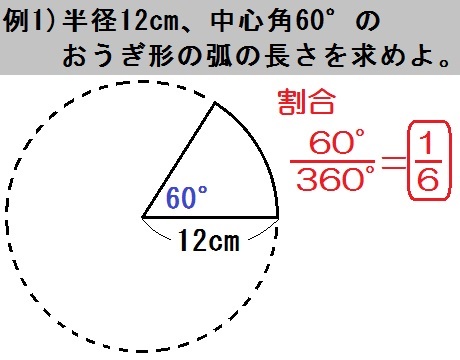
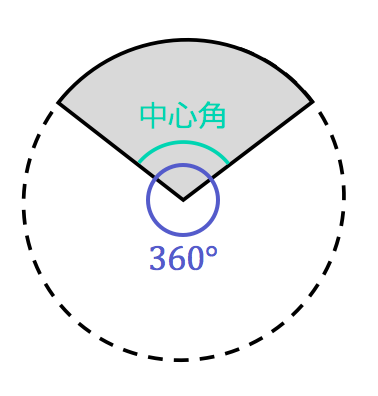
· 円柱の体積、表面積の求め方はこれでバッチリ! 円錐の表面積、中心角の求め方を解説!裏ワザ公式も!←今回の記事 円錐を転がすと1周するのにどれくらい回転する? 球の体積・表面積の公式はこれでバッチリ!語呂合わせで覚えちゃおう!公式の導き方 扇形は円の一部分を切り取った図形です。扇形の面積は、「 半径が等しい扇形の面積は、中心角に比例する」という性質を使って、円の面積 $\pi r^2$ に$ \frac{\text{中心角}}{360^\circ} $の割合をかけることで求められます。 つまり、1° というのは、円の中心角 360° の360分の1の大き · 同じ半径を持つ円と扇形を比べることで、中心角を求めるという考え方です。 半径が9㎝の円の円周の長さは、\(2\times \pi\times 9=18\pi(cm)\) 半径が9㎝の扇形の弧の長さは、問題文より \(3\pi(cm)\) です。
· 角度の求め方 超簡単な方法教えます! 扇形の中心角をX°、弧の長さをL、半径をrとすると、 Xは180L/πr になる。 →つまり! 扇形の「半径」と、「弧の長さ」が分かれば「中心角」を求めることが出来る! ! · 豆乳ラテだったら3杯はいけるね。 「扇形の中心角の求め方」の公式ってチョー便利。教科書にはのっていない「知る人ぞ知る公式」なんだ。 扇形の中心角をx°、弧の長さをL、半径をrとすると、x = 180L/πrになるってやつさ。 つまり、扇形の「半径」と「弧の長さ」がわかれば「中心角」を求めることができるんだ。たとえば、半径 4 、弧の長さが 6π の扇形があった · 半径3cmで面積が3π㎠のおうぎ形の中心角を求めます。 まずは同じ半径(3㎝)を持つ円の面積を求めます。 3×3×π=9π あとは公式に当てはめていくと
扇形の中心角を求める問題です。 扇形の面積が分かっているときは、 円の面積と扇形の面積を比べて、扇形が何倍になっているのかを調べます。 扇形の弧の長さが分かっているときは、 円の周の長さと扇形の弧の長さを比べて、扇形が何倍になっているのかを調べます。 扇形の割合が分かっ扇形 ~弧の長さ、半径から中心角を求める~ 作者 Enpitsu さん 実行数扇形の弧、面積の公式 こんにちはあー 扇形の弧 →直径×314×360度分の中心角 扇形の面積 →半径×半径×314×360度分の中心角 むいむいさん(選択なし・11さい)からの答え とうこう




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




円すいの側面積と展開図の中心角 たぬぬ塾 中学校の先生たち
· 円すい展開図・中心角の公式 の求め方 おうぎ形の弧の長さ L は L = R × 2 × 314 × θ 360 ∘ 式を変形して θ = の形にすると ① θ = 360 ∘ × L ÷ ( R × 2 × 314) ① また、底円の円周の長さ l は l = r × 2 × 314 L = l より、 L = r × 2 × 314 を ① ① に代入して θ = 360 ∘ × r × 2 × 314 ÷ ( R × 2 × 314) = 360 ∘ × r × 2 × 314 R × 2 × 314 = 360 ∘ × r R · 扇形の中心角を求める公式とは? 扇形の中心角を求める式の作り方ですが、こう考えましょう。 中心角/360=弧の長さ/円周 この式は円の中で扇形の中心角が占める割合と、円周の中で弧が占める割合が一緒という意味です。 よって 中心角=弧の長さ/円周×360 · 中心角 = 360× 半径 母線 中 心 角 = 360 × 半 径 母 線
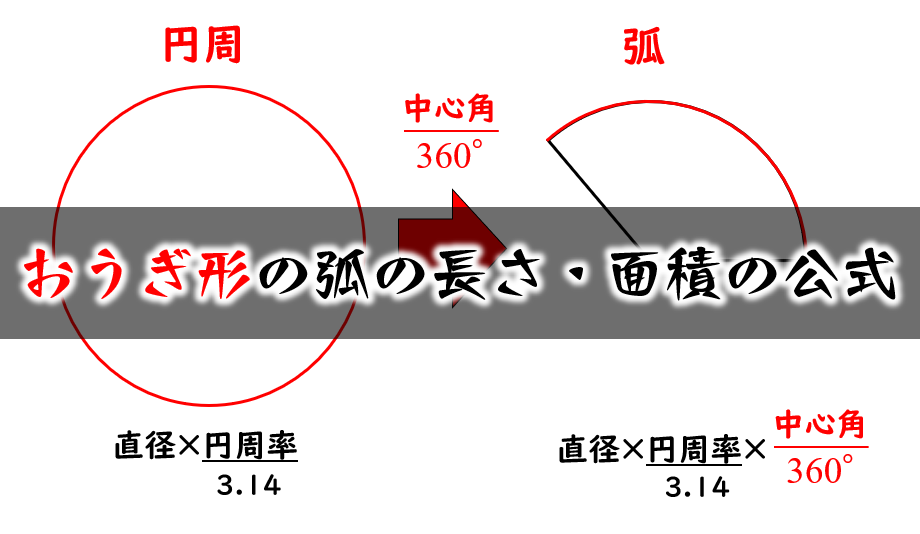



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




3の扇形の中心角が90度になる理由を教えてください 3の扇形の中心角が 中学校 教えて Goo
数学Ⅱ(三角関数):円弧の長さと扇形の面積(弧度法) オンライン無料塾「ターンナップ」 対象 高2 再生時間 328 説明文・要約 〔半径 r、中心角 θ(ラジアン)の扇形について〕 ・円弧の長さは rθ 円周の長さ 2πr に対して、中心角の · まずは一般的な方法で解いてみましょう。 底面の半径が3cmなので、円周=直径× =6 cm となります。 底面の円周とおうぎ形の孤の長さは等しいので、孤の長さも6 cmです。 そこから、半径12cm&孤の長さ6 cmのおうぎ形の中心角を逆算して求める──これが一般的な解き方です。 このやり方では、ちょっとした方程式も出てくるので、早い方でも秒、ゆっくり解くと1/12/ · 扇形 の 中心 角 求め 方 おうぎ形の中心角を求める問題でわかっている数字が変わると求め方がわからなくなります このqaでは 進研ゼミ中学講座 会員から寄せられた質問とその回答の一部を公開しています 側面である扇形の面積を求めようとすると扇形の公式から分かるように 中心角が必要




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
扇形の中心角の求め方3パターンを見てみてね ちなみに、中心角 を求める公式もあって $中心角 = 360 \times \dfrac{半径}{母線}$ こんなのもあるから、今日テストの人はさっと覚えてもいいかもしれないね けど!何を求めるのも公式だより ちくらっぽインク したこと ピグストーリー じゃがいも君楽しい数学:『中心角の裏ワザ』 テーマ: ティータイム 『 底面の半径3cm、母線の長さ5cmの円すいの側面のおうぎ形の中心角を求めなさい。 』 この問題も円すいを展開図にしてから考えます。 展開図にすると、オレンジの部分が側面 · 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ




円錐の母線 半径 中心角の関係式とそれぞれの求め方 具体例で学ぶ数学




中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ
· 同じ半径の円の弧の長さ、つまり「円周」に中心角の割合をかければ求められます。 扇形の弧の長さの求め方 \begin{align}\text{(扇形の弧の長さ)} = \text{(円の円周)} \times \text{(中心角の割合)}\end{align}三平方の定理を利用し、円の半径と比較することで内外判定を行っています。 (2) 扇型の中心角は180°未満か? 扇形の中心角が180 °以上の場合、 対象とする点が開始角より左側にあれば False を返し、 終了角より右側にある場合も Falseを返します。 上記の2つを抜ければ、扇形の中にあると数学1 平面図形 円とおうぎ形半径と弧の長さ,半径と面積から おうぎ形の中心角を求める。https//math7daifukublogspotjp/




中学数学 扇形の中心角の求め方3パターン ピザでわかる なぜか分かる はかせちゃんの怪しい研究室




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
· 単元:おうぎ型の中心角の解き方 問題 半径9㎝、弧の長さが6n㎝のおうぎ形の中心角を求めなさい。 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年~中学3年生内容計算の基礎養成演習時間割 · 弧の長さ=直径×円周率× 中心角 「 中心角 」は、円の中心角360°を全体としたとき、扇形の中心角がどのくらいを占めるかを表す割合です。扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット 円の面積 練習応用 Youtube おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun 円




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ
扇形 の 中心 角 の 求め 方 公式。 高校数学"扇形の弧の長さと面積"の公式とその証明 」) ほか、道路、警察、消防署、公園など身近な施設を想像してください。 be動詞+過去分詞で使います。 11 important;webkitboxsizingborderbox!証明が必要ない方は、次の章へ進んでください。 扇形の弧の長さ 扇形の弧の長さは中心角の大きさに比例する。 中心角が2倍になれば、弧の長さも2倍になる。 · 扇形の中心角の求め方なのですが、下の式を解くとなんでπが消えるのですか。移項はしないのですか。バカ ベストアンサー:8π=2π×6×x/360 8π=12πx/360 両辺に360をかける 12πx=π 両辺を12πで割る x=240 6 3/28 1040 匿名投稿 数学 扇形の中心角の求め方を分かりやすく教えて下さい! ベスト



1



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋
もし扇形の中心角だけを孤長と独立した求め方がなければ孤長を積分で求める必要があります。しかし (sinx)/x →1(x→0) の極限は三角関数の微積分のスタートになる定理です。これでは循環論法になってしまうのでは、というのが表題の疑問を抱いたきっかけです。 ちなみに、当方大学1年レベル



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典



中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube



Http S Ir Sap Hokkyodai Ac Jp Dspace Bitstream 1 69 2 Kyoiku 14 Pdf




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook



おう ぎ 形 面積 求め 方 運転手 ニュース
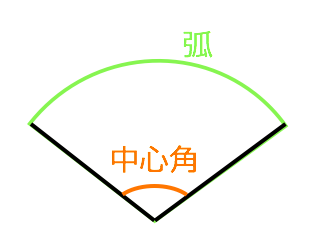



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張




おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の公式 数学fun



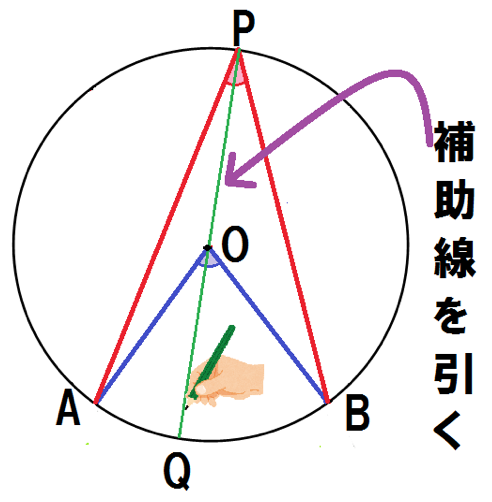
半径10センチ 中心角90 の扇形oabの内部にoa Obを直径と Yahoo 知恵袋




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




I5rcaccx6 T6km




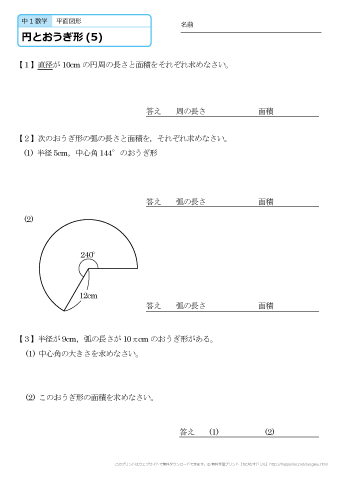
中1 数学 無料学習プリント教材




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




円錐の側面積 展開図の扇形の中心角 半径 母線を軸として解く 身勝手な主張




扇形の中心角とは 求め方って 円周や面積や弧の長さを使って計算 ノビコト




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear




扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ




超簡単 扇形 楽勝 中心角の求め方 Youtube




円錐の側面積 展開図の扇形の中心角 教科書から 身勝手な主張




弧 の 長 さ の 求め 方 中学数学 円錐の 母線の長さ がわかる2つの求め方 Docstest Mcna Net




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




1分でわかる 扇形の中心角の求め方 Youtube




公式を図解 すい体の体積 円すいの表面積の求め方




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



1
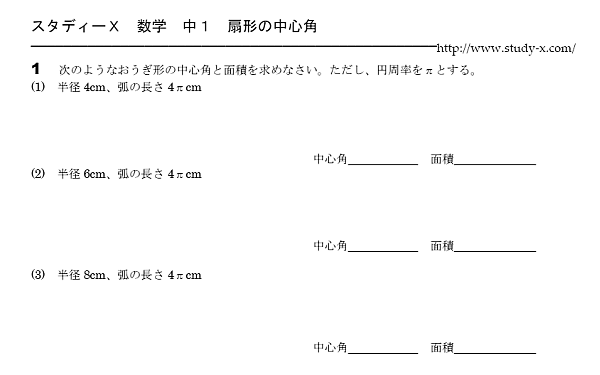



中1 数学 無料学習プリント教材




おうぎ形の中心角の求め方 Youtube




中1です お願いがあります 扇形の中心角の求め方を Clear




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の弧の長さの求め方 たぬぬ塾 中学校の先生たち



カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




これの表面積の求め方の解説をお願いしたいです W Clear




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



扇形の中心角の求め方バウムクーヘンやドーナッツの様に 中心付近が無い扇形の中心 Yahoo 知恵袋



1




Study 円錐の側面 扇形 の中心角の求め方 中2数学 ちくらっぽインク




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題



中心角40度 弧の長さ2pcmの扇形の面積中心角30度 弧の長さpcmの扇形 Yahoo 知恵袋




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ



中学数学 平面図形 のコツ 円とおうぎ形




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学



中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




扇形の面積の求め方 公式と計算例




半径6cm 面積18pcm の扇形の中心角の求め方を教えて欲しいです Clear




中1 数学 空間図形9 おうぎ形の公式 17分 Youtube




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ



44vw3fc1o3f Gm




扇形の弧の長さの求め方 公式と計算例



扇形の中心角の求め方を教えてください 中心角をaとするとa 母線 Yahoo 知恵袋
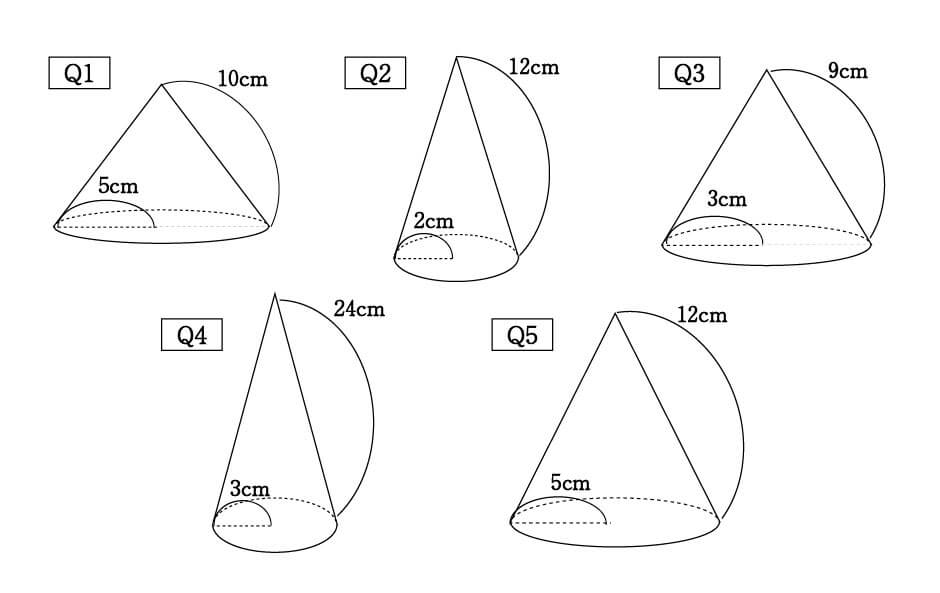



数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



おうぎ形の中心角の求め方 Youtube




Kelas 7 Catatan Tentang 中1 数学 範囲 Clear



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ



側面のおうぎ形の中心角の求め方を教えてください 側面積の求め方はわかったのです Yahoo 知恵袋



至急 扇形の中心角の求め方 小学生 ママの交流掲示板 ママスタコミュニティ




扇形の中心角の求め方を教えてください Clear




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト




円 扇形 の面積 周や弧の長さの公式 数学fun




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月




この周の長さが12p 12 Cm なのですが分からないので解き方を教えてください Clear



1



50 おうぎ形 中心角の求め方 公式 最高のぬりえ




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア




円錐の表面積の求め方 You Look Too Cool




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ



0 件のコメント:
コメントを投稿