三角形の重心の座標の求め方とその証明 数学ii By ふぇるまー マナペディア
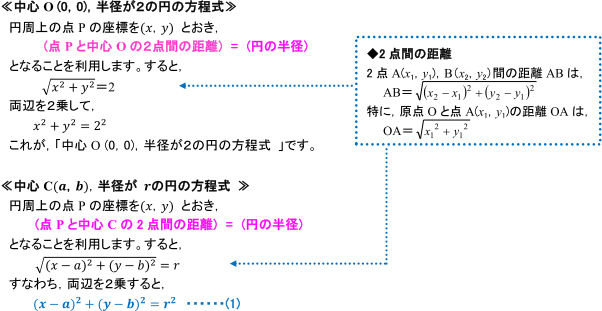
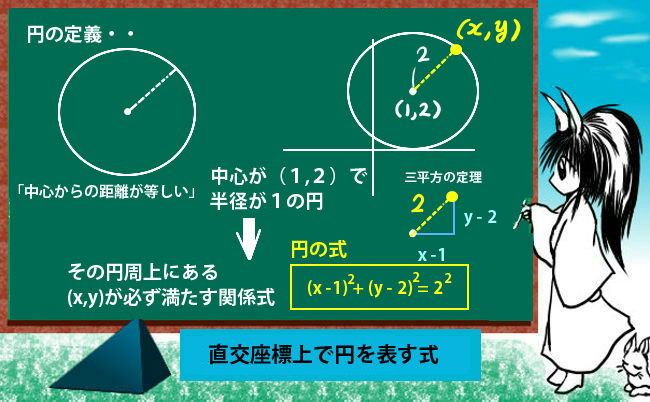
円の方程式とは？ 円の方程式とは、 中心の座標と円の半径を用いて、円を方程式で表したもの です。 表し方には「基本形」と「一般形」の \(2\) 通りがあります。 基本形の公式 円の方程式を基本形で表現すると、円の中心と半径が一目でわかります。まず、球の中心の座標を求めましょう。球は3次元ですので、中心座標は(x,y)ではなく(x,y,z)となることに注意しましょう。 このやり方は例を見ながら考えると理解しやすいでしょう。中心座標(x,y,z)が(4, 1, 12)の球があるとしましょう。この座標を使って、数
円 中心 求め方 座標
円 中心 求め方 座標-2点間の距離 = 半径×2 → 中心が1つ（1点目と2点目に同じ座標が表示される）重心とは何か？ 座標を使って重心を求める方法物理 高校の力学で学ぶ重心。 なんとなく意味はわかるものの、求め方はわからないという人が多いのではないでしょうか？ 重心の求め方は一通りではないため、テキストをたくさん見れば見るほど
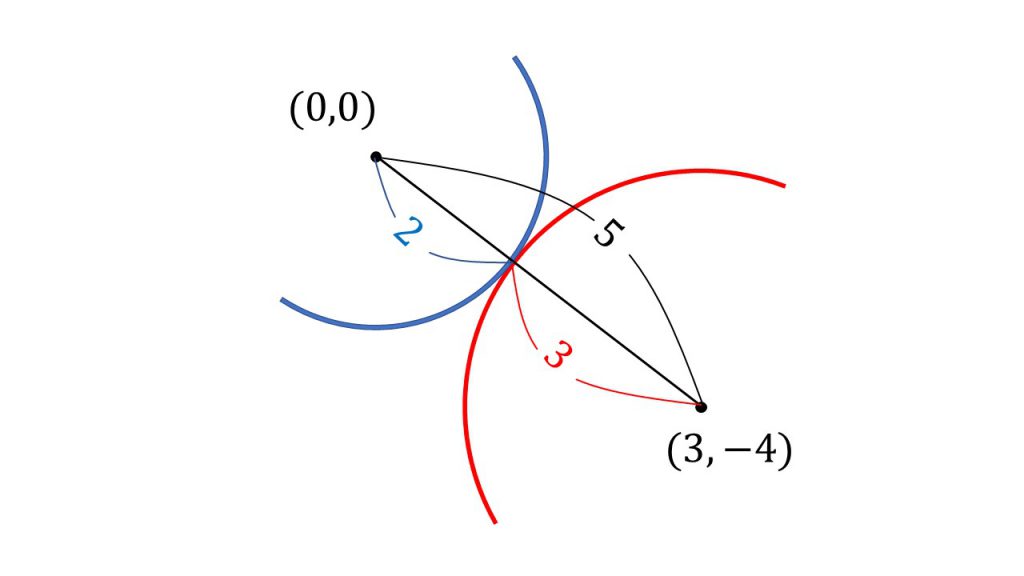
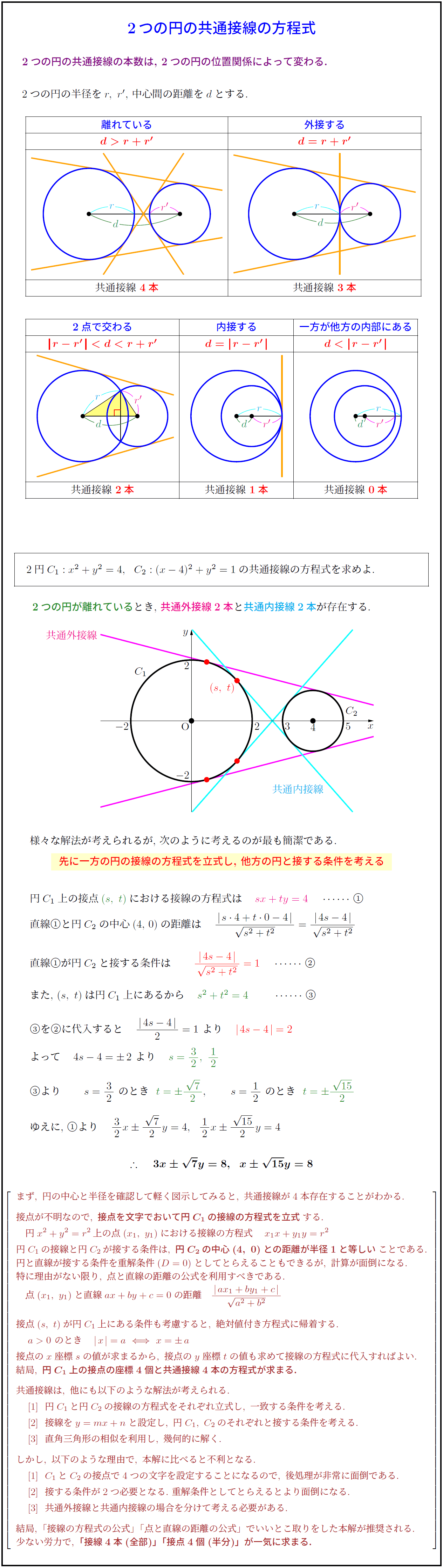
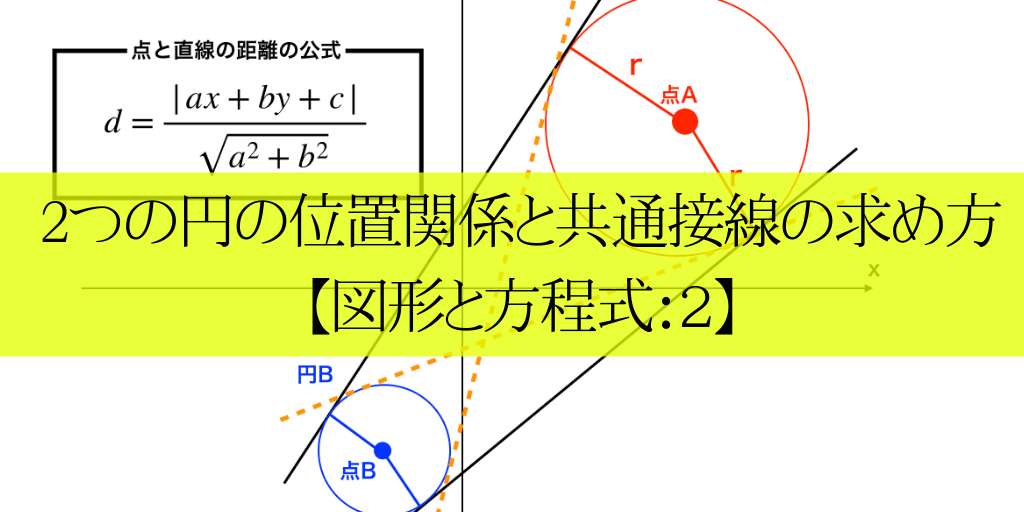
2つの円の位置関係 大学受験の王道
つまり、 軸上で円と重なる点を求めましょう。 ↓の図で言うと点cと点dです。 では実際に、点cと点dの値を求めましょう。 円の中心の座標が(50,0)、円の半径が150なので、三平方の定理例として，中心が (0, 0) (0,0) (0, 0) で半径が 2 2 2 の円の方程式を考えます。そこで今回は、すでに描いた円の中心点を簡単にだす方法をご紹介させていただきます。 円の中心点を簡単に出す方法 今回使用するJw_cadの便利な機能は『 クロックメニュー 』という機能です。 まずは、キャプチャー動画で操作手順をご確認ください。
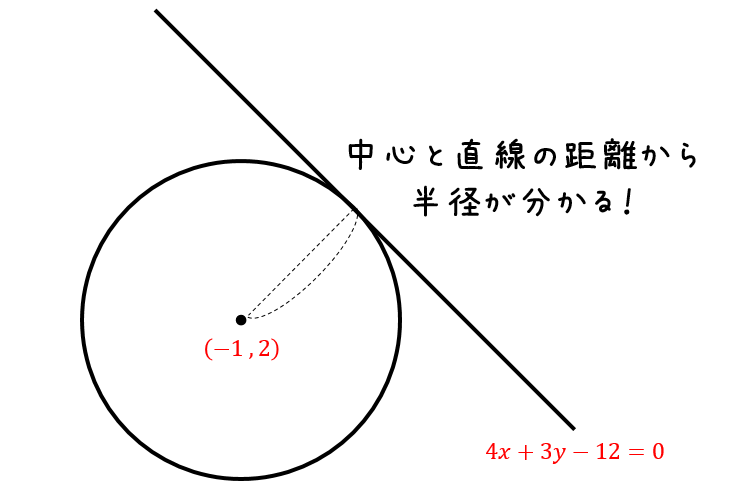
を中心とした半径 の円と、直線 の交点を考えます。 上の図で、点hの座標は「点と直線の距離を求める」で求めました。 と置けば、点hの座標は次のように書けます。 次に線分hqの長さを考えます。この長さは三平方の定理から簡単に求めることができます。求めたい円弧の半径を X とします。円弧の幅を W とし、高さを H とします。求める X はピタゴラスの定理から上の式のようになります。これを展開したものが下の式です。 この X を半径 R として、円弧の両端から円を描き、その交点 C が円弧の中心です。2円(円弧)に接する内接円の中心座標の求め方 2円(円弧)に接する内接円の中心座標の計算式をどなたか教えてください。例・a円r2250_中心座標(x00y1563) b円r700_中心座標(x0y00) c円r300の場合の計算式を教えてください。 上記、例ですと内接するc円は、2個
円 中心 求め方 座標のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 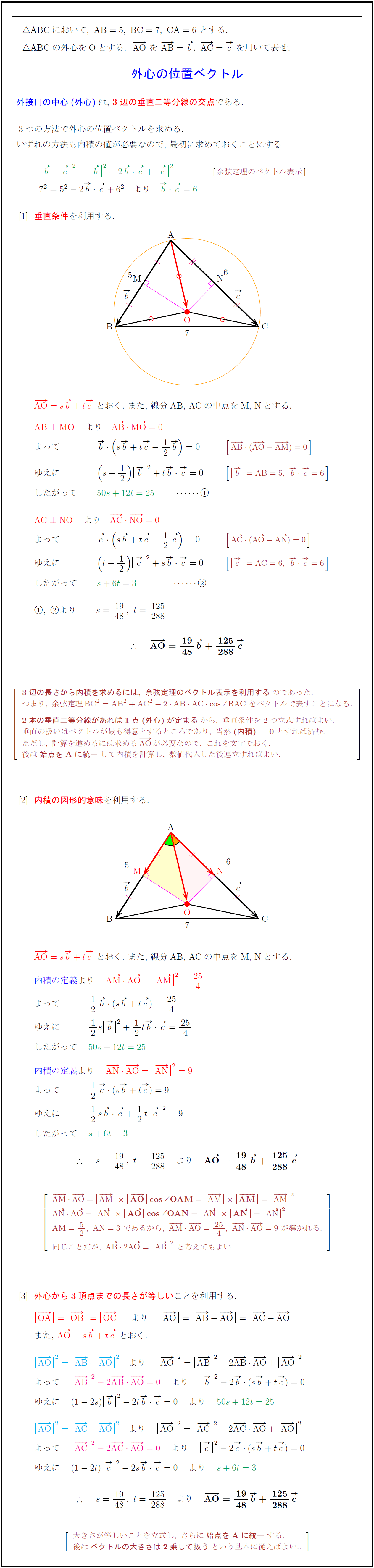 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
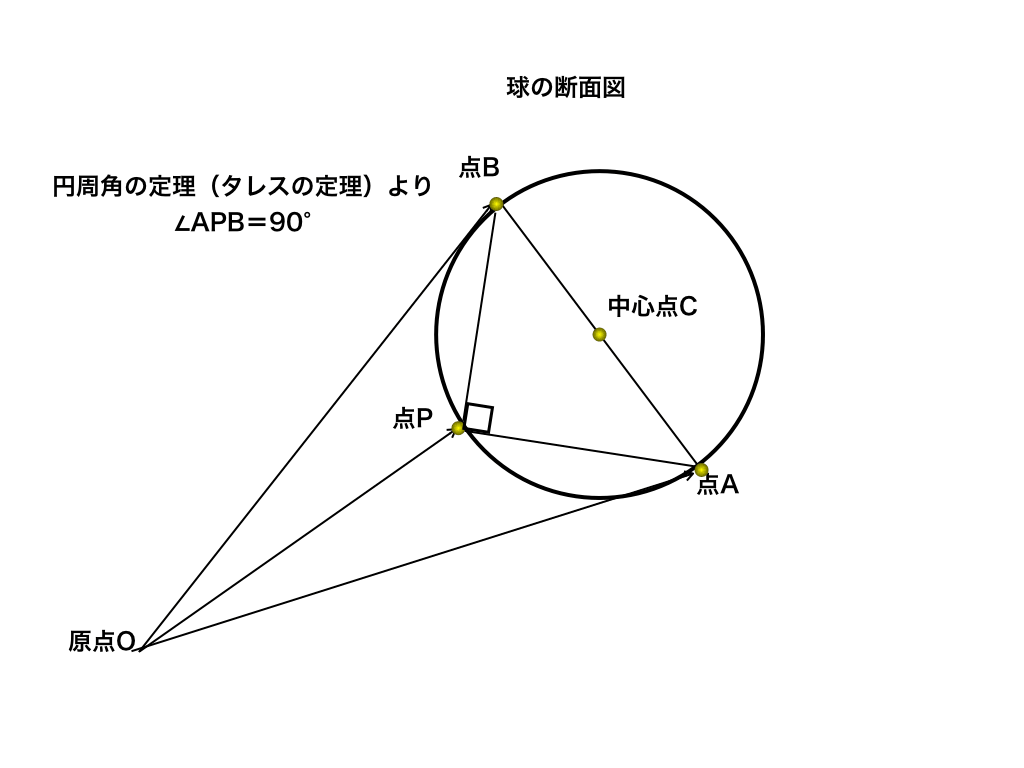 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 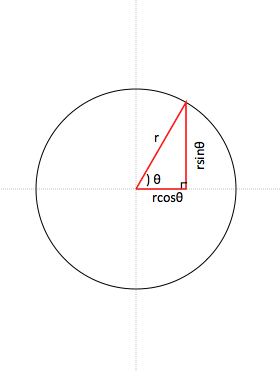 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 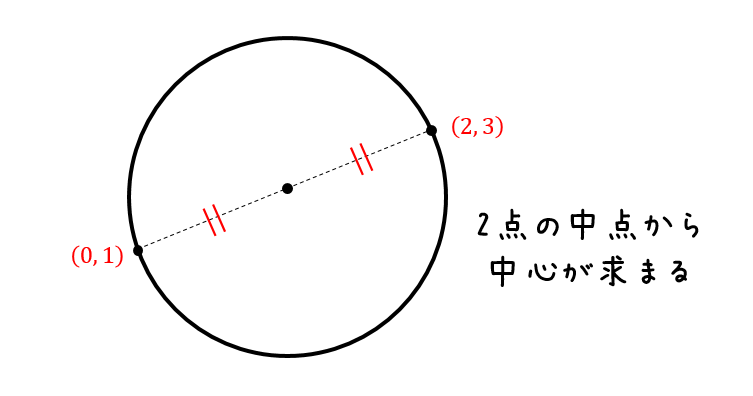 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 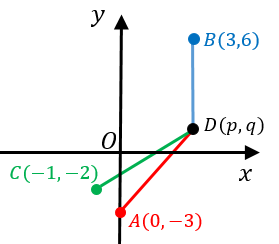 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 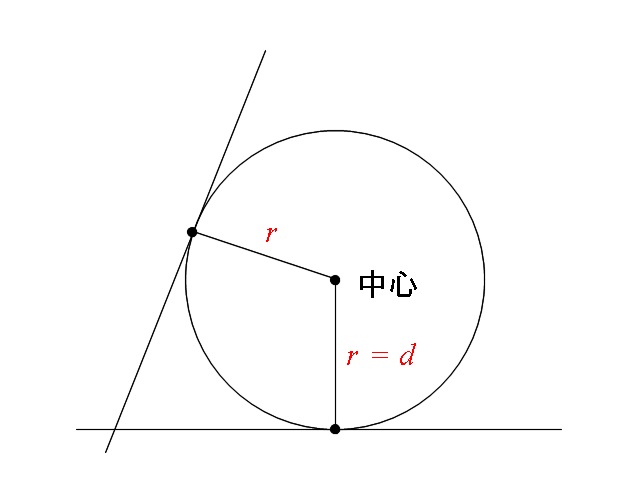 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
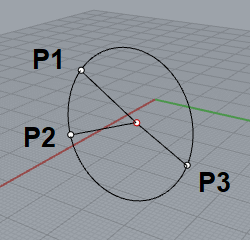円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
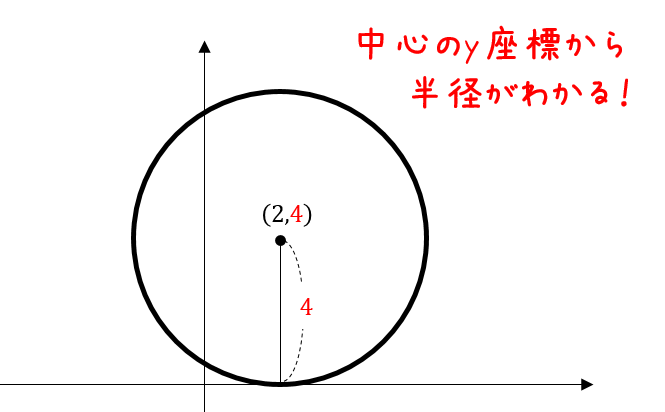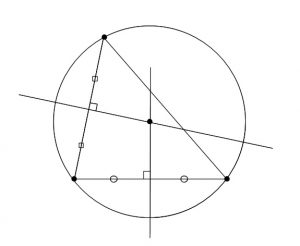 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |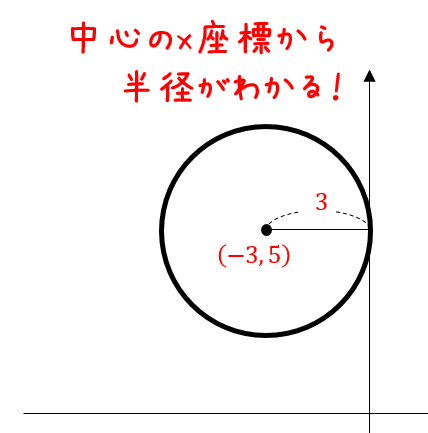
円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 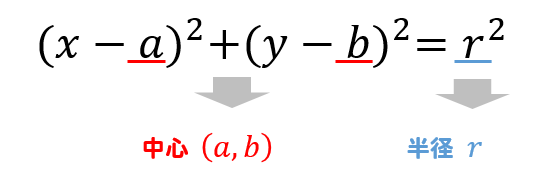 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 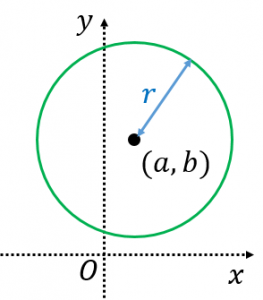 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
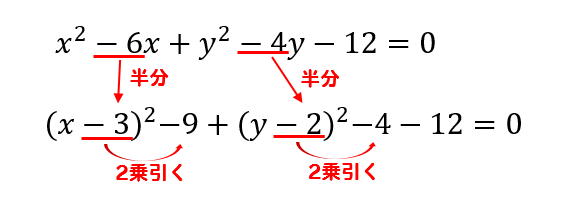 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 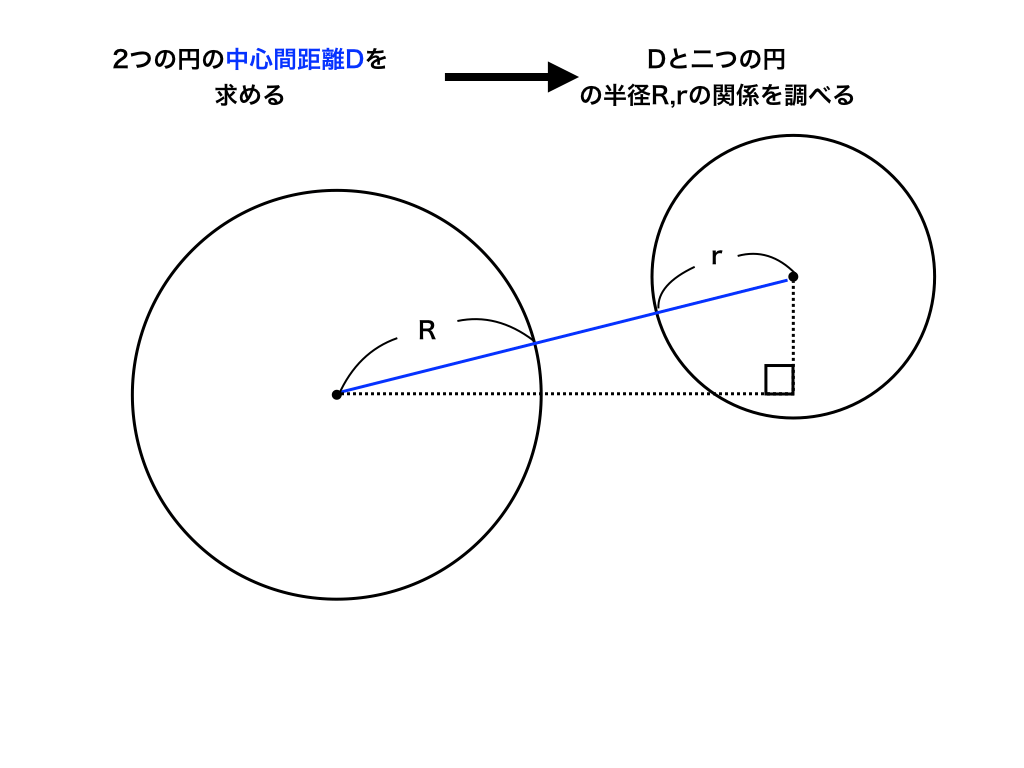 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 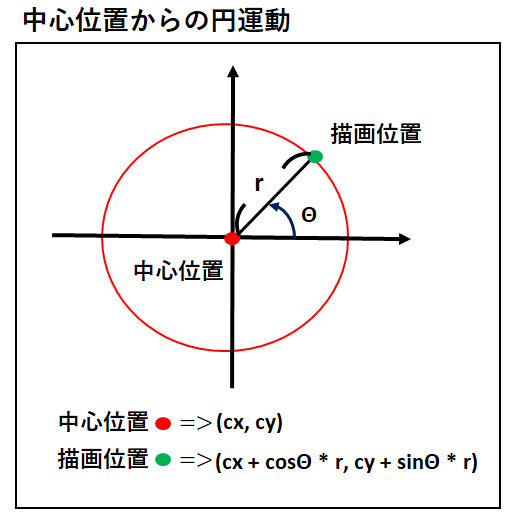 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |  円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
「円 中心 求め方 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 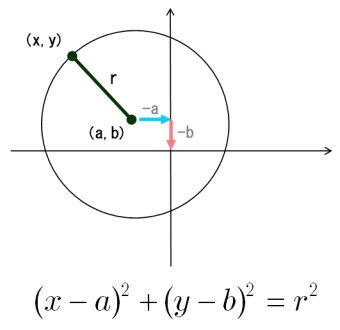 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 | 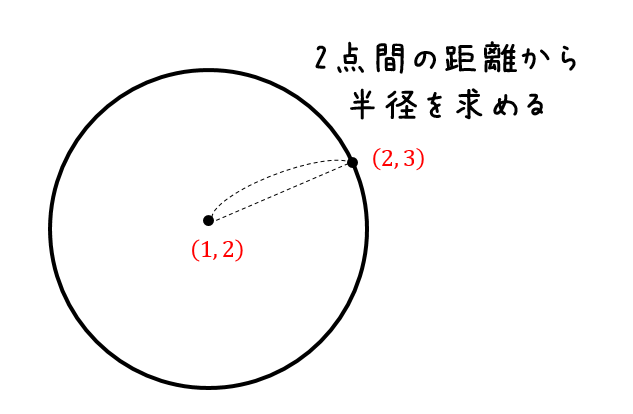 円の方程式とは 公式 接線 微分 や半径の求め方 計算問題 受験辞典 |
一直線上にない任意の3点が与えられれば、その3点を通る円を求めることができます。 ここでは、任意の3点を通る円の中心座標と半径を求める方法を2種類の方法で紹介します。 なお、以下では、円の方程式を、 とし、点が円の中心点の座標、が半径とします。3点を通る円の中心を求める解法はわかりますが、4点以上の多点を通る場合は、どのような求め方があるでしょうか？どなたかわかる方アドバイス願います。#3の続きです。e=(xa)^2(yb)^2r^2を展開して、e = 2ax 2by a^2b^2r^2
Incoming Term: 円 中心 求め方 座標,
0 件のコメント:
コメントを投稿